Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 20

Имеются два граничных условия: Т = Т₀ при х = 0 и Т = Т₁ при х = l. Использование их дает возможность найти константу интегрирования и величину q. В результате

T = (T₀^3/2 + (T₁^3/2 – T₀^3/2)×x/l)^2/3,

q = – 2c/3T ^1/2×(T₁^3/2 – T₀^3/2)/l.

3.5. Тепло, выделяющееся во внутреннем цилиндре, проходит через газ (задача решается в приближении сплошной среды; после решения может быть сделана еще оценка, подтверждающая применимость приближения) и уходит как через боковую поверхность внешнего .цилиндра, так и через его торцевые поверхности. В случае длинных цилиндров торцевые поверхности составляют малую часть от боковой и теплообменом через них можно пренебречь: считать, что цилиндры бесконечно длинные. Поскольку задача имеет осевую симметрию, то ее решение определяется одной единственной координатой, радиусом r. В силу стационарности, сколько тепла выделяется во внутреннем цилиндре, столько его за то же самое время проходит через любую поверхность, охватывающую источник тепловыделения и лежащую между цилиндрами. Если эту поверхность выбрать в виде коаксиального цилиндра радиуса r (r₁ ≤ r ≤ r₂) и q(r) – плотность.потока тепла по нормали, то

(l - длина цилиндра).

Для сплошной среды плотность теплового потока вычисляется по формуле

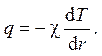
Коэффициент теплопроводности по элементарной  кинетической теории равен

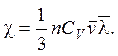
Здесь C_V = 5k/2 (колебательное движение молекул азота при рассматриваемых температурах заморожено),   – средняя длина свободного пробега. Легко видеть что c в первом приближении не зависит от плотности газа и пропорционален корню квадратному из температуры:

 где

После подстановки c и q уравнение для т примет вид

Интегрирование его, с учетом граничных условий Т = т₁ при r = r₁ и Т = т₂ при r = r₂, дает

Коэффициент теплопроводности находится по формуле

или приближенно

Для газокинетического диаметра молекулы получается выражение

Расчет для азота дает

3.6. Благодаря цилиндрической симметрии задачи плотность потока тепла q не зависит от угла, она функция только радиуса r. Поэтому полный поток тепла через боковую поверхность произвольного цилиндра радиуса r (r < R) равен произведению площади этой поверхности на плотность потока тепла 2prlq. Из закона сохранения энергии в стационарном случае полный поток тепла через боковую поверхность равен полному теплу, которое выделяется в единицу времени внутри выбранного цилиндра. В противном случае температура внутри цилиндра будет изменяться. Итак,

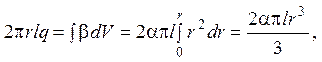
откуда

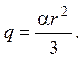
По закону Фурье

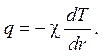
В результате для нахождения температуры получаем обыкновенное дифференциальное уравнение первого порядка

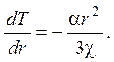
Интегрирование его при условии r = R, T = T₀ приводит к искомому распределению температуры в объеме

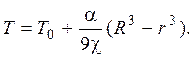
3.7. Рассматривается стационарное течение. Цилиндрический канал длинный, что позволяет не учитывать влияние концов его. Жидкость несжимаемая. В результате можно считать, что имеется лишь одна компонента скорости жидкости (обозначим ее через u), направленная вдоль оси x. Эта компонента скорости зависит только от расстояния до оси симметрии (радиуса r). Градиент давления постоянный, имеет отрицательное значение. Течение ламинарное.

В области течения выделяется цилиндрический слой жидкости между радиусами r и r + dr. Жидкость не испытывает ускорения, Поэтому равнодействующая всех сил, действующих на жидкость в выделенном объеме равна нулю. Рассмотрим проекцию всех сил на ось x. По цилиндрической поверхности радиуса r действует сила трения t2prl|_r, где t – напряжение трения, нижний индекс указывает, на каком расстоянии  действует сила трения. По цилиндрической поверхности радиуса r + dr сила трения действует в противоположном направлении –t2prl|_r + dr. На торцевые поверхности действуют силы давления. С учетом заданного перепада давления проекция этих сил на ось x равна Dp2prdr. Балансовое уравнение имеет вид