Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 14

С другой стороны, по формуле Больцмана

ΔS = k ln (W₂ / W₁).

Приравняв эти два выражения для ΔS, можно найти

W₂ / W₁ = exp (Q / k × (T₁^–1 – T₂^–1)).

Если Q = 1 эрг = 10 ^–7 Дж, W₂ / W₁ » exp(10¹²/12) » . Чудовищно большое значение этого отношения говорит о том, что именно такой переход всегда и происходит. Обратный же переход никогда не наблюдается.

Однако, если Q = 1,2×10^–12 эрг, то W₂ / W₁ » exp (0,1) » 1. Таким образом, происходят оба перехода с примерно одинаковой вероятностью.

2.1. Энергия линейного гармонического осциллятора определяется формулой

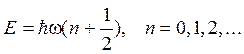
Тогда для первой системы выполняется уравнение

E₁ = (n₁ + n₂ + 1) = 

и, следовательно, n₁ = n₂ = 0. Первоначально первая система находится в единственном квантовом состоянии, ее энтропия равна нулю: S₁ = 0.

Аналогично для второй системы

E₂ = (n₃ + n₄ + 1) = 

Отсюда n₃ + n₄ = 2. Возможные комбинации значений квантовых чисел n₃ и n₄ следующие:

Три различные комбинации – три различных состояния системы. Первоначальное значение энтропии второй системы S₂ = k×ln 3.

Полная энергия объединенной системы равна

E = E₁ + E₂ =

После установления теплового контакта между исходными системами энергия может быть локализована на любом из четырех осцилляторов, что отображается уравнением:

E₁ = (n₁ + n₂ + n₃ + n₄ + 2) = 

откуда n₁ + n₂ + n₃ + n₄ = 2. Возможные комбинации значений квантовых чисел объединенной системы определяются из приведенной ниже таблицы.

n1	2	0	0	0	1	1	1	0	0	0
n2	0	2	0	0	1	0	0	1	1	0
n3	0	0	2	0	0	1	0	1	0	1
n4	0	0	0	2	0	0	1	0	1	1

Всего 10 различных комбинаций, и, следовательно, 10 разных состояний полной системы. Ее энтропия равна S = k×ln 10. Результирующее изменение энтропии полной системы

DS = S – S₁ – S₂ = k×ln (10/3).

2.2. При фиксированных внешних параметрах уровни энергии остаются неизменными. Подвод теплоты Q приводит к изменению распределения частиц по уровням энергии. В результате средняя энергия системы увеличивается. Средняя энергия определяется выражением

До подогрева она равна = –m₀ B×0.9 + m₀ B×0.1 = –0.8m₀ B, после подогрева = –m₀ B×0.6 + m₀ B×0.4 = – 0.2m₀ B (здесь учтено, что вероятность находиться системе на нижнем уровне энергии выше). Поглощаемая системой теплота равна Q = –  = 0.6m₀ B.

2.3. Система A и A¢ (из трех и двух спинов соответственно) образуют полную систему A₀. Энергия взаимодействия между спинами пренебрежимо мала, так что полная энергия равна сумме энергий систем A и A¢:

E₀ = – (M + M¢)B,

где M и M¢– их магнитные моменты.

Система A₀ состоит из пяти спинов и поэтому обладает 2⁵ = 32 возможными состояниями, каждое из которых может быть обозначено квантовыми числами s₁, s₂, s₃ (для первой системы A) и s¢₁, s¢₂ (для системы A¢). Эти квантовые числа указывают ориентацию магнитных моментов отдельных спинов. Энергия изолированной системы A₀ равна

E₀ = –3m₀ B.