Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 6

Результаты приведены в таблице в строке № 2.

3) В случае изотермического процесса f ( p,V ) = pV =const (следует из термического уравнения состояния). Изменения внутренней энергии не происходит, так как температура газа остается постоянной ( DU = 0). Согласно первому началу термодинамики, работа, а, следовательно, и подведенная теплота равны ( A = Q). Выражая давление через объем посредством термического уравнения состояния ( p = RT/V), в результате получаем:

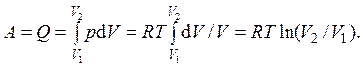
Соответственно, при постоянной температуре изменение энтропии будет равно

DS = Q/T = Rln(V₂/V₁).

Из определения теплоемкости следует, что в изотермическом процессе ее величина будет бесконечно большой: ненулевое подведенное тепло при нулевом изменении температуры. Результаты для изотермического процесса приведены в строке № 3 таблицы.

4) Адиабатический процесс – это равновесный процесс без подвода теплоты: dQ = 0. Изменения энтропии в соответствии со вторым началом термодинамики не будет:

.

 Теплоемкость C = 0. Изменение внутренней энергии в этом процессе, как и в других процессах, равно DU = C_VDT (не зависит от процесса). По первому началу,  совершаемая работа

A = – DU = ­­– C_VDT.

Остается найти уравнение процесса. Его можно получить из первого начала термодинамики в дифференциальной форме. После подстановки в него dQ = 0, dU = C_V dT и dA = pdV имеем дифференциальное уравнение

C_V dT + pdV = 0.

Исключение температуры с помощью термического уравнения состояния дает

dT = d( PV ) = PdV + VdP,

C_V /R×Vdp + (C_V /R + 1)pdV = 0, или Vdp + g pdV = 0,

где g = C_p/C_V – показатель адиабаты. Уравнение решается разделением переменных. Это дает уравнение адиабатического процесса

pV ^g = const.

Результаты для адиабатического процесса представлены в строке № 4 таблицы.

5) Политропическим называется процесс с постоянной теплоемкостью. Она считается известной. Тогда

Q = CDT.

Изменение энтропии находится аналогично случаю изохорического и изобарического процессов с единственным изменением в теплоемкости процесса:

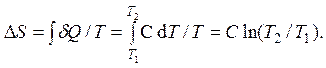
По-прежнему, DU = C_VDT. В таком случае работа

A = Q –DU  = (C – C_V)DT.

Уравнение процесса находится, как и для предыдущего процесса.

C dT = C_V dT + pdV.

Аналогично исключается температура:

dT = d( PV ) = PdV + VdP,

C_V /R×Vdp + (C_V /R + 1)pdV = С(PdV + VdP).

Вводится обозначение n = (C – C_p)/( C – C_V) – показатель политропы.  Как и в случае адиабатического процесса, здесь производится группировка слагаемых при приращении одинаковой переменной, после чего уравнение решается разделением переменных. После интегрирования находится уравнение политропического процесса

pVⁿ = const.

Результаты для этого процесса заполняют строку № 5 таблицы.

№	f	A	Q	DU	DS	C
1	V	0	CVDT	CV DT	CV ln(T2/T1)	CV
2	p	RDT	CpDT	CV DT	Cp ln(T2/T1)	Cp
3	pV	RTln(V2/V1)	RTln(V2/V1)	0	Rln(V2/V1)	±¥
4	pVg	– CV DT	0	CV DT	0	0
5	pVn	(C – CV)DT	CDT	CV DT	C ln(T2/T1)	C

1.2. При отклонении от положения равновесия, в котором координату xбудем полагать нулем, на поршень действует направленная вдоль оси x сила F_x = (p₀ – p) S, где p – давление в закрытой части цилиндра.