3.5. Для измерения теплопроводности газа им заполняется пространство между двумя длинными коаксиальными цилиндрами радиуса r1 и r2. Заполнение производится при невысоком давлении (~ 10 мм рт. ст.), чтобы исключить конвекцию. Внутренний цилиндр нагревается источником тепла с удельной мощностью Q, установившиеся температуры цилиндров t1 и t2 измеряются. Найти коэффициент теплопроводности исследуемого газа. Рассчитать газокинетический диаметр молекулы для азота, если r1 = 0.5 см, r2 = 2 см, Q= 0.038 вт/см, t1 = 93 ˚C, t2 = 0 ˚C.
3.6. Внутри цилиндрического объема радиуса R с теплоизолированными торцами выделяется теплота. Причем плотность выделения ее в единицу времени, зависит от расстояния от оси цилиндра по закону b = αr, где α – постоянная. Найти распределение температуры в объеме. Температура внешней боковой поверхности объема поддерживается постоянной равной T0. Коэффициент теплопроводности c постоянный.
3.7. Найти профиль скорости v и расход жидкости j (вытекающий за единицу времени объем) при ламинарном течении жидкости в трубе. Радиус трубы r0, длина l, на концах трубы поддерживается разность давлений Dр.
3.8. Определить, на какой угол j повернется диск, подвешенный на упругой нити, если под ним на расстоянии h = 1 см вращается второй такой же диск со скоростью w = 50 рад/с. Радиусы дисков r = 10 см, модуль кручения нити a = 100 дин×см/рад, коэффициент внутреннего трения воздуха h = 1,8 ×10–4 пуаз. Краевыми эффектами пренебречь. Движение воздуха между дисками считать ламинарным. Каков будет угол поворота верхнего диска в случае, если диски поместить в камеру, из которой воздух откачивается до давления р = 10–4 мм рт. ст.?
3.9. В тонкостенном сосуде с гелием объема V имеется малое отверстие площадью s. Как будет изменяться давление внутри сосуда, если вначале оно равно давлению окружающего воздуха?
ОТВЕТЫ
1.2.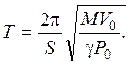 
1.3.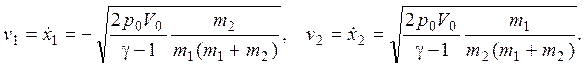 
1.4. A¢ = 2CV T0(2(g - 1)/2 - 1), C = – CV.
1.5. а) A¢ = p0 V0/(g – 1)×(2g – 1 + (2/3)g – 1 – 2),
б) A¢ = 2p0 V0/(g – 1)×((4/3)(g – 1)/2 – 1).
1.6. C = 2R.
1.7. A = C1T10 + C2T20 – (C1 + C2)
.
1.8. Q1 = Q3×T1/T3×(T2 - T3)/(T1 - T2) » 38 Вт.
1.9. Q/Q1 = (T1 – T3)T2/(T2 – T3)/T1 ≈ 7,1.
1.12. ΔU = nCVT0(2g – 1 – 1), ΔS = nR×ln 2.
1.14. pV = RT,
U = bT + c,
S = – a +b + b∙lnT + R∙lnV,
CV = b, Cp = b + R.
1.16. U = n(
dT - an/V
+ const),
S = n(dT/T + R×ln(V/n
- b) + const).
1.17. a = CV(T2 – T1)V1V2/(ν(V1 – V2)) ≈ 0,42 Дж∙м3/моль2.
1.18. ΔS = mcv×ln((T1 + T2)2/4T1 T2) > 0, ΔU = 0,
ΔF = mcv×ln(
).
1.19. q = (cт – cж)T1×ln(T0/T1) + q0T1/T0.
2.1. DS = k×ln (10/3).
2.2. Q = 0.6m0B.
2.3.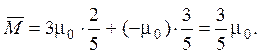 
2.4. w(–3m0) = 1/7, w(+m0) = 6/7, w(+3m0) = w(–m0) = 0.
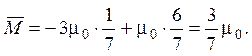
2.5.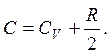 
2.6. dw(vx, vy) = m/2pkT × exp(– m(vx2 + vy2)/2kT) dvx dvy,
dw(v, j) = m/kT × exp(– mv2/2kT) v dv × dj/2p.
= m
/2 = kT.
2.7. 
= (πkT/2m)1/2.
2.8. p = jmv0/2πR.
2.9. j = n/π.
2.10. 
= (9pkT/8m)1/2, 
= 2(kT/m)1/2, 
j = 2kT.
2.11. F = nkTs(1 – (1 + (r/l)2)–3/2).
2.12.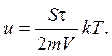 
2.13. 
2.14. (
)max = 2β.
2.16. p = N(mg)3/(kT)2/(2p tg2a), 
=
3kT.
2.17. = 9kT/4.
2.18.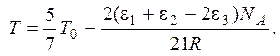 
2.19. Е = Nhn×cth(hn/2kT), CV = 2Nk (hn/2kT)2/sh2(hn/2kT).
2.20. lmax = 6.
2.21. 
= e0 + De/(1 + (g0/g1)×exp(De/kT)),
CV = R(g0/g1)×(De/kT)2×exp(De/kT)/(1 + (g0/g1)×exp(De/kT))2,
N0 = N/(1 + (g1/g0)×exp(–De/kT)), N1 = N – N0.
2.22. c = M /Н = (2m02n/kT)/(3 + exp(DЕ/kT)).
2.23.
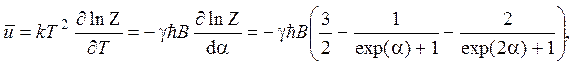
где
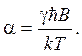
3.1. ν = 
N/S
∙2d, где = (πkT/2m)1/2.
3.2.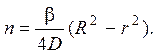 
3.3.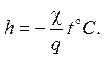 
3.4. T = (T03/2 + (T13/2 – T03/2)×x/l)2/3,
q = – 2c/3T 1/2×(T13/2 – T03/2)/l.
3.5. c = 3Q/4p×ln(r2/r1)(T13/2 – T23/2)–1T 1/2 »
» Q/2p×ln(r2/r1)(T1 – T2)–1,
»
0,9 × 10–4 Дж/(см×с×К),
» 3,6
.
3.6.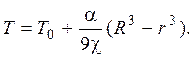 
3.7. v = Dр(r02 – r 2)/(4lh), j = pDр r04/(8lh).
3.8. j » 0,015 рад. при p = 10–4 мм рт. ст. < p0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.