j = phwr4/2ah = 81°
при p >> p0; . 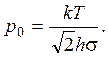
3.9. р = р0
(1 + exp(– t/tHe)
– exp(– t/tвозд)), t
= 4V/(s![]() ).
).
Решения
1.1. Уравнение каждого процесса ищем в виде:
f ( p, V ) = const.
Обычно вид этой функции находится из первого начала термодинамики в дифференциальной форме
dQ = dU + dA,
где dQ – подведенная к системе теплота, dU – изменение внутренней энергии, dA – работа системы.
Но чтобы получить искомое уравнение процесса, в выражение для дифференциальной формы первого начала необходимо подставить конкретные выражения для dU, dAи dQ. Так как исследуемая система – идеальный газ, то для одного моля идеального газа мы имеем:
- термическое уравнение состояния p V= RT,
- калорическое уравнение состояния U =CVT
- выражение для работы dA = PdV.
- полученное системой тепло
связано с теплоемкостью исследуемого равновесного процесса C определением: 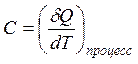
Для одного моля идеального газа в соответствии с законом Менделеева-Клапейрона (термическим уравнением состояния) давление p равно
p = RT/V,
где R – универсальная газовая постоянная.
Калорическое уравнение состояния для идеального газа имеет вид
U = U(T).
Работа газа при изменении его объема от V1 до V2 равна
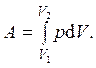
Подведенное к системе количество теплоты Q при теплоемкости C равно
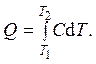
Теплоемкость в процессе, в котором сохраняется величина x, определяется как
Cx = (¶Q/¶T)x.
Внутренняя энергия – функция состояния. Ее изменение не зависит от процесса, а определяется только начальным и конечным состояниями системы. По первому началу термодинамики (в интегральной форме) изменение внутренней энергии системы при переходе ее из одного равновесного состояния в другое состояние равно
DU = Q – A.
Для равновесных процессов согласно второму началу термодинамики дифференциально малое изменение энтропии определяется равенством
dS = dQ/T= CxdT/T.
1) Для изохорического процесса (процесса с постоянным объемом) функция f ( p,V ) = V= const. Теплоемкость газа равна CV. По условию, эта теплоемкость постоянна. Поэтому, согласно определению теплоемкости
Q = CVDT .
С другой стороны, при постоянном объеме работа газа равна нулю, и, согласно первому началу термодинамики, вся подведенная энергия должная перейти в изменение внутренней энергии газа:
DU = Q.
На основе двух последних соотношений получаем выражение для внутренней энергии:
DU = CVDT.
Так как бесконечно малое количество подведенной к газу теплоты в рассматриваемом процессе равно dQ = CV dT, то изменение энтропии
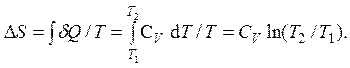
Полученные для данного процесса результаты занесены в приведенной ниже таблице в строку под номером № 1.
2) Для изобарического процесса (процесса с постоянным давлением) функция f ( p,V) = p =const. Работа вычисляется с использованием прямого определения для работы газа A = pdV с последующим применением уравнения состояния pV = RT:
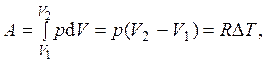
где DT = T2 – T1.
Согласно определению, теплоемкость газа равна Cp ( p = const, следовательно, x = p). Количество подведенной к газу теплоты Q = CpDT.
Так как внутренняя энергия идеального газа зависит только от температуры (не зависит от объема), то приращение DU будет таким же, как и в предыдущем процессе, т. е. DU = CVDT (не будет лишним напомнить, что U – функция состояния).
Если в первое начало термодинамики подставить найденные выражения для A, Q и DU, то получится соотношение Майера
A = Q – DU ® Cp DT – CV DT = RDT ® Cp – CV = R.
Оно получено для идеального газа и справедливо только для него.
Выражение для приращения энтропии может быть получено так же, как и выше для изохорического процесса. Единственное отличие заключается в другой теплоемкости процесса: СP вместо CV:
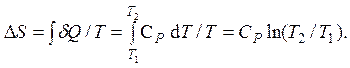
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.