Линейная динамическая система с заданными коэффициентами характеристического уравнения будет устойчивой и все корни будут лежать в левой полуплоскости, если значения всех коэффициентов таблицы Раусса больше или равно нулю.
Если для коэффициентов Раусса выполняются строгие неравенства:
,
то линейная динамическая система будет асимптотически устойчивой.
Решение Гурвица.
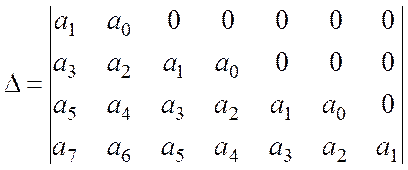
Для решения задачи рассматриваются главные миноры:
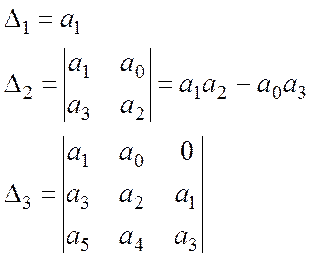
Теорема Гурвица:
Динамическая система будет устойчива и все корни будут лежать в левой полуплоскости, если все коэффициенты матрицы Гурвица и определители главных миноров положительны.
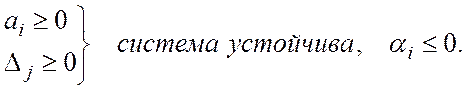
Динамическая система будет асимптотически устойчивой и
все корни вещественной части строго меньше нуля, если выполняются строгие
неравенства: 
.
Связь решений Раусса и Гурвица.
Раусс:
;
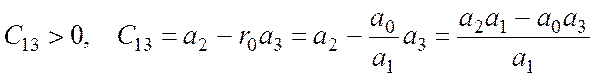– условия Гурвица.
Практическое использование.
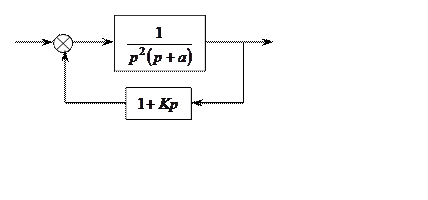
Выбрать К.
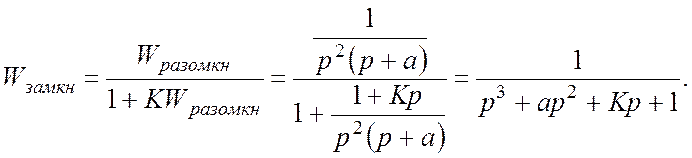
Характеристическое
уравнение: 
.
Матрица:
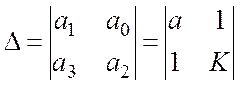
Условия
Гурвица: 
.
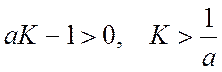Статические и астатические системы передаточной функции по управлению, возмущению и ошибке.
Астатические свойства разомкнутой системы формируются дифференцирующим звеном, которое обеспечивает нулевые значения нулей системы.
.
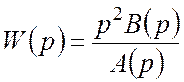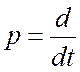–оператор Лапласа.
–дифференцирующее звено.
Допустим, что на техническую систему с данной передаточной функцией действует постоянное входное воздействие.
,
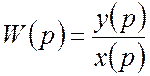–константа.
Асимптотическая система по отклонению входной переменной при любом ее постоянном значении обеспечивает постоянный нулевой сигнал на выходе.
.
Система называется астатической по отклонению и по
скорости, если ее передаточная функция содержит два дифференцирующих звена 
. В этом случае при любых коэффициентах 
и 
отклонение
выходного сигнала равно нулю.
Астатическая система сохраняет положение равновесия при любых постоянных возмущающих воздействиях и для нее выполняются показатели устойчивости по отношению к возмущающим воздействиям.
.
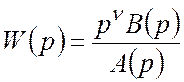–степень астатизма.
–астатическая система по отклонению,
–астатическая система по скорости,
–астатическая система по ускорению.
Передаточные функции по управлению, возмущению и ошибке.
.
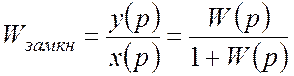–передаточная функция
по управлению.
Если в качестве управляющего воздействия рассматривать
входную величину 
и в качестве выходной 
, то передаточная функция замкнутой системы
представляет собой передаточную функцию по управлению.
.
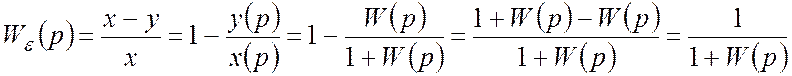Астатическая система в случае замыкания единичной обратной связью.
Рассмотрим передаточную функцию разомкнутой системы, содержащую несколько интегрирующих звеньев.
.
.
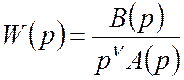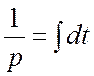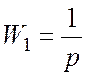–интегрирующее звено.
.
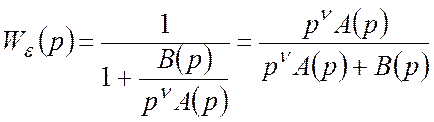В случае замыкания единичной отрицательной обратной
связью передаточной функции, содержащей интегрирующих
звеньев будет создана астатическая система по ошибке порядка . То есть астатическая система отслеживает
идеально с нулевой ошибкой входной сигнал 
.
.
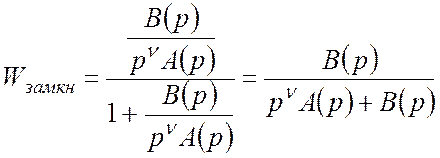Передаточная функция по управлению является статической по управлению, если не содержит дифференцирующих звеньев.
Для технических систем характерны разные точки входа управляющего и возмущающего воздействия.
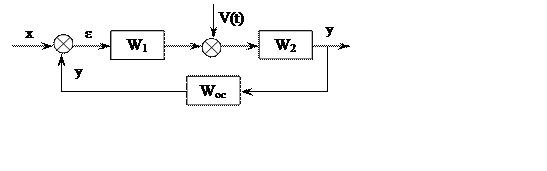
Для данной структурной схемы следует определить передаточную функцию по управлению, возмущению и ошибке.
По управлению: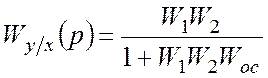 
.
По ошибке:
.
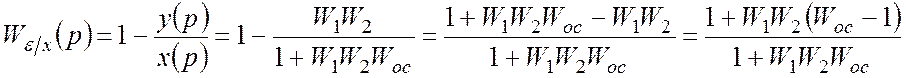По возмущению:
.
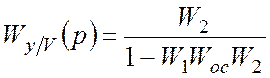Для создания астатической системы могут быть использованы интегрирующие и дифференцирующие звенья.
Астатизм по ошибке:
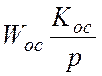, где 
–коэффициент обратной связи.
.
,
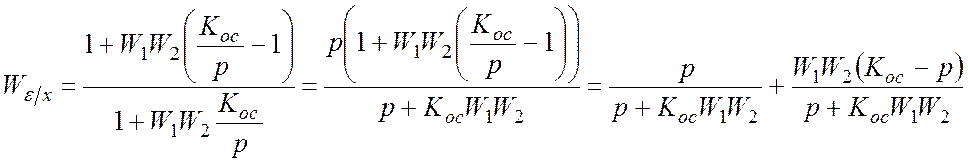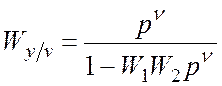– астатизм по
возмущению.
В случае единичной отрицательной обратной связи
выберем 
:
.
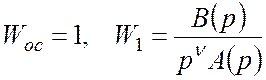Астатизм по ошибке:
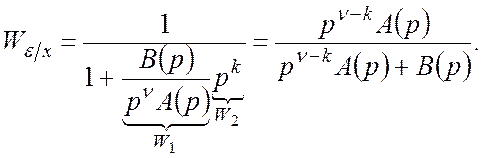
При выборе корректирующих звеньев, обеспечивающих
прохождение управляющего сигнала через интегрирующее звено 
и возмущающего сигнала через
дифференцирующее звено, могут быть обеспечены следующие свойства технической
системы:
1. Статические свойства по отношению к управляющему сигналу.
2. Астатические свойства по отношению к возмущающему воздействию.
3. Астатические свойства по ошибке, если число интегрирующих звеньев в прямой цепи больше числа дифференцирующих звеньев.
Синтез линейных многоконтурных систем управления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.