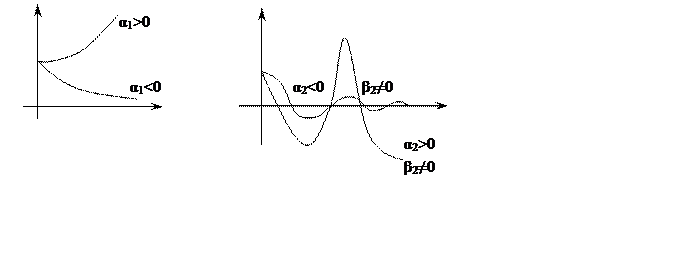
Если все корни характеристического уравнения имеют отрицательную вещественную часть и расположены в левой полуплоскости, то это условие является необходимым и достаточным для устойчивости динамической системы в силу понятия об устойчивости при начальных отклонениях.
Если имеется хотя бы один неустойчивый корень с положительной вещественной частью, то и вся динамическая система неустойчива.
Качественный и количественный анализ устойчивости динамической системы по значениям корней характеристического уравнения.
1. Качественный анализ устойчивости.
2. Число форм движения.
– общее число форм,
– корней вещественного
типа 
,
– корней комплексно –
сопряженных 
.
,
.
Для динамической системы определяется число форм
движения с корнями вещественного типа и число
форм движения колебательного типа с комплексными корнями .
Общее число форм движения равно сумме форм движения с вещественными и комплексными корнями.
3.
Характеристика движения по
формам в порядке возрастания 
и убывания 
.
На данном этапе анализа определяются обобщенные показатели:
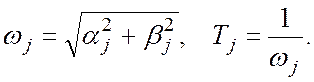
Затем указывается характер движения по первой форме и запасы устойчивости по величине вещественной части корня.
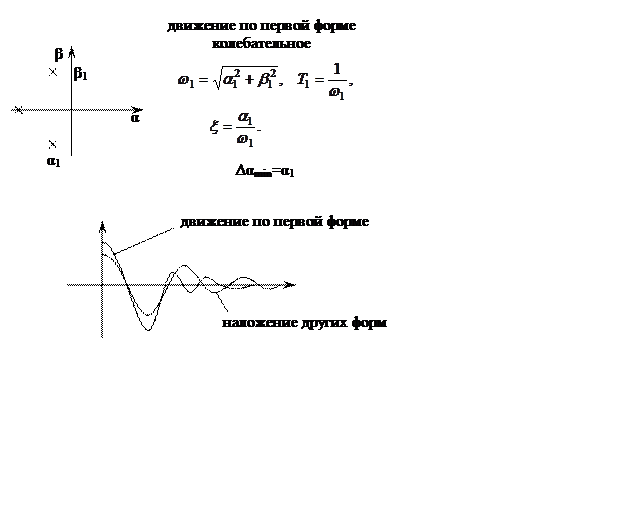
Характеристика длиннопериодического и короткопериодического движения.
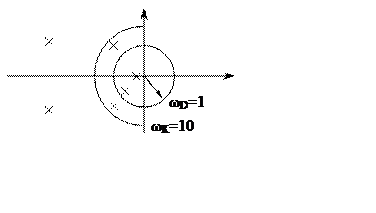
В зависимости от типа самолета определим на
комплексной плоскости области расположения корней внутри окружности радиусом 
, внутри кольца с радиусами и 
, в
оставшейся области.
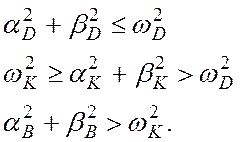
В соответствии с расположением корней относительно выбранных границ в динамике движения определяют следующие формы:
1. Короткопериодическое движение.
Частота короткопериодического движения обычно составляет несколько Герц (1-5 Гц). Примерами короткопериодического движения является движение по углу тангажа, по перегрузке, по углам крена, рыскания и атаки.
2. Длиннопериодическое движение.
Длиннопериодическое движение происходит с частотами, равными десятым и сотым долям Герца и описывает движение самолета по высоте, скорости, углу наклона траектории, боковой дальности.
3. За границей короткопериодического движения расположены частоты быстрого колебательного движения, связанного с аэро–упругими колебаниями. Частота колебательного движения при деформации конструкции самолета составляет от нескольких (5-10 Гц) до 100 и более. Такое колебательное движение иногда называют вибрацией.
В соответствии с разделением корней принимается гипотеза о «замороженном» движении длиннопериодических переменных в процессе изменения тех координат, которые описывают короткопериодическое движение. Изменение высоты, скорости, угла наклона траектории не учитываются, и сами переменные считаются постоянными за время изменения короткопериодических составляющих: угла атаки, перегрузки и т.д.
При расчете длиннопериодических координат самолет считается сбалансированным в угловом движении и по перегрузкам. Для расчета движения центра масс используются усредненные значения перегрузки и балансировочные значения углов.
Характеристическое уравнение системы в целом:
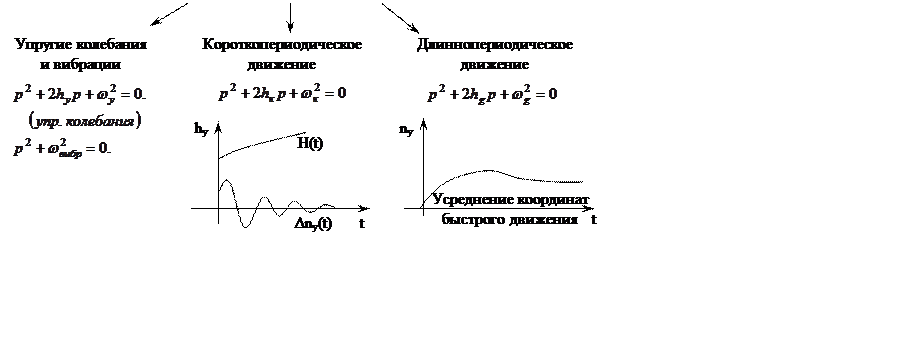
Для решения практических задач с использованием Matlab используются стандартные программы.
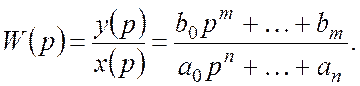
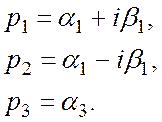
Алгебраические критерии устойчивости Раусса и Гурвица.
Выбор критериев алгебраической устойчивости определяется постановкой следующей задачи:
определить алгебраические показатели, которые зависят только от коэффициентов характеристического уравнения и позволяют судить об устойчивости динамической системы и отсутствии неустойчивых корней.
Дано:
Требуется: 
Решение Раусса:
|
№ строк |
Номер столбца |
||||
|
1 |
2 |
3 |
4 |
||
|
1 |
a0 |
a2 |
a4 |
a6 |
|
|
2 |
a1 |
a3 |
a5 |
a7 |
|
|
r0=a0/a1 |
3 |
C13=a2-r0a3 |
C23=a4-r0a5 |
C33= |
|
|
r1=a1/a3 |
4 |
C14=a3-r1C23 |
C24=a5-r1C33 |
C34= |
|
Теорема Раусса:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.