3)Использование цифровых систем управления приводит к дискретности измерений управляющих сигналов по времени и по уровню.
Дискретность по времени зависит от параметров разрядной сетки.
Задачи исследования н./л. САУ:
1)Определение характеристик устойчивости системы с нелинейными элементами.
2)Определение режимов устойчивости автоколебаний; амплитуды и частоты автоколебаний.
3)Исследование устойчивости цифровых систем и анализ влияния дискретных факторов на ЛАФЧХ всей системы.
Исследование устойчивости технических систем, описываемых нелинейным ДУ.
Анализ н./л. САУ включает определение следующих характеристик:
1)Положение равновесия, вычисленного на основе решения нелинейных алгебраических уравнений:
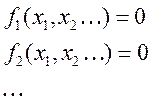
В качестве примера рассмотрим зависимость коэффициента момента тангажа от угла атаки.
|
Число положений равновесия определяется типом нелинейных функций и количеством корней системы нелинейных уравнений. Проблемы решения нелинейных систем состоят в определении промежутков, на которых находятся корни, в отделении действительных корней от мнимых. Корни отыскиваются с помощью ЧМ с заданной точностью.
2)Для управляемых нелинейных динамических систем вычисляются балансировочные зависимости управляющей переменной от фазовых координат.
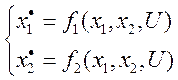
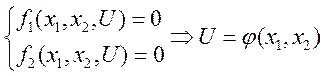
Если подставлять различные значения U из допустимой области, то каждому значению U будет соответствовать набор значений Xi – при заданном U.
В качестве примера приведем
построение балансировочной зависимости руля высоты от скорости и высоты полета.
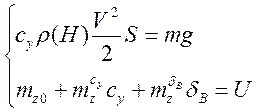
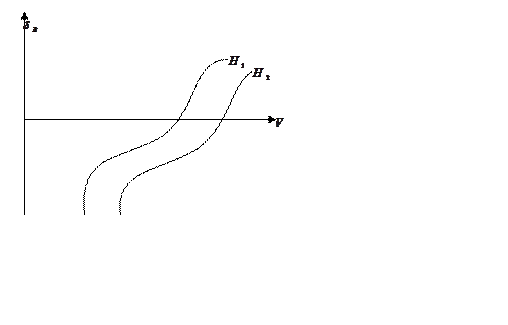
Практическое приложение балансировочных зависимостей охватывает построение возможных областей полета из условий балансировки сил и определения отклонения рулей от режима полета.
3)Исследование устойчивости режимов балансировки и динамической системы на области возможных изменений фазовых координат.
Для нелинейных ДС определяется положение устойчивого и неустойчивого равновесия и устойчивость циклических колебаний.
-
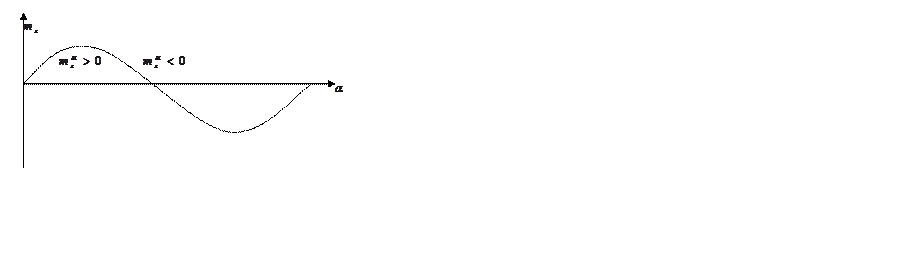
неустойчивость
-
устойчивость
Метод фазовой плоскости
Метод фазовой плоскости использует следующую процедуру исследований:
1)Задаются значения(начальные) фазовых координат на основе метода сеток:
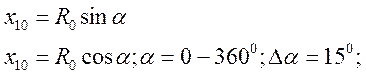
2)Для каждого начального значения фазовых координат интегрируют нелинейную ДУ и траектория строится на фазовой плоскости.
Построенная траектория называется портретом нелинейной ДС.
Исследование фазовых портретов позволяет определить устойчивое и неустойчивое положение равновесия.
Для нелинейных систем характерны автоколебания, которые определяются амплитудой и частотой.
Для нелинейных систем используются следующие понятия:
1)Нелинейная ДС и ее состояние
Xо называется устойчивым в малом, если существует такое
, что верны неравенства:
2)Нелинейная ДС называется
асимптотически устойчивой в -окрестности положения
равновесия, если:
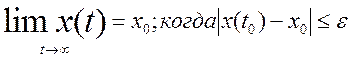
3)Нелинейная ДС ограничено
устойчива на интервале времени 
, если за время движения
отклонение от положения равновесия не превышает 
:
при 
4)Нелинейная ДС называется устойчивой в большом если, при любых начальных отклонениях, она возвращается к устойчивому положению равновесия.
5)ДС называется устойчивой на области значений фазовых координат, если можно указать граничные значения, превышение которых приводит к потере устойчивости, а любое положение внутри границы обеспечивает переходный процесс к устойчивому положению равновесия.
6)Нелинейная ДС называется устойчивой в целом, если на всей области фазовых координат для данной системы существуют устойчивые положения равновесия и устойчивые предельные циклы колебаний.
Теорема Ляпунова об устойчивости нелинейных систем.
Рассматривается система нелинейных уравнений вида:
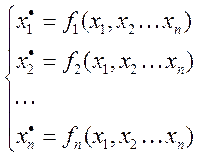
Метод Ляпунова представляет собой подбор функции Ляпунова, обладающей следующими свойствами:
1)Функция Ляпунова является
положительно определенной на области значения фазовых координат
2)Для исследования устойчивости необходимо определить знак производной от функции Ляпунова.
1)
2)
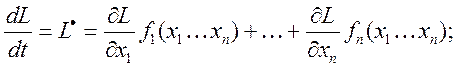
Теорема Ляпунова:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
