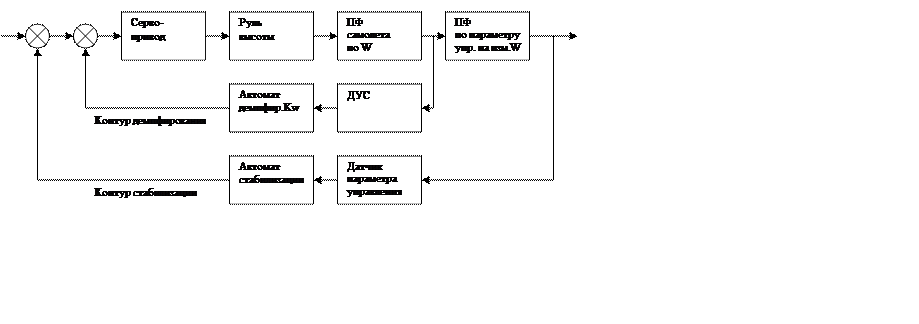
Оба контура в совокупности составляют СУ самолетом.
 Для управления движением самолета рассматриваются
следующие задачи:
Для управления движением самолета рассматриваются
следующие задачи:
1) Определение ПФ автомата демпфирования, автомата стабилизации и автомата управления траекторным движением для обеспечения необходимых запасов по амплитуде и по фазе в каждом контуре.
При решении данной задачи ПФ самолета, привода и датчиков считать известными.
В курсовой работе принять ПФ датчиков=1, а ПФ привода описать колебательным звеном.
2) Определить программы настройки коэффициентов усиления автоматов демпфирования, стабилизации и управления траекторией по скоростному напору в области возможных режимов полета при выполнении требований к постоянству частоты и относительного коэффициента демпфирования.
Для статически устойчивого самолета на практике выбор коэффициента обеспечивается на основе наращивания устойчивых контуров по заданным запасам устойчивости.

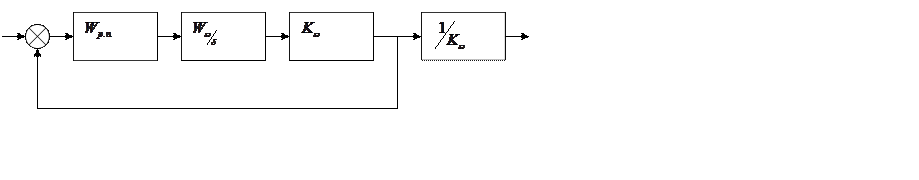

При выборе привода его
постоянная времени выбирается в 10 раз меньше, чем постоянная времени самолета
и округляется до значения определенного ряда.
(0.05;0.02;0.01),(0.2;0.15;0.1) 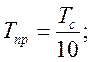
Привод состоит из двигателя и ротора. Сервопривод имеет жесткую и гибкую обратные связи и отслеживает угол поворота и угловую скорость.
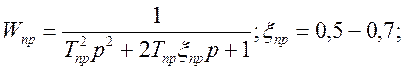
Для создания устойчивого контура демпфирования выбирают коэффициент усиления автомата демпфирования по требуемой величине коррекции амплитудной характеристики.
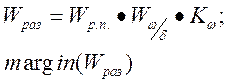
При синтезе системы с использованием MatLab необходимо учитывать допущения классической ТАУ:
1)Все критерии устойчивости, критические точки и запасы устойчивости в целях определенности установленной для передаточной функции с положительным коэффициентом усиления и случая превышения порядка полинома знаменателя над порядком полинома числителя.
2)Для ПФ с положительным коэффициентом усиления корректирующего звена является отрицательная обратная связь.
3)Запасы устойчивости по амплитуде и по фазе определяются по характеристикам разомкнутой системы для единичной, отрицательной обратной связи.
![]()
![]()


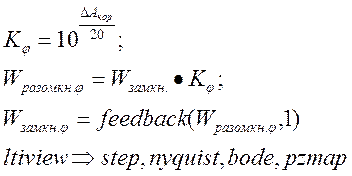
Для каждого контура определяются значения запасов устойчивости по амплитуде и по фазе по характеристикам разомкнутой системы.
Характеристики переходных процессов и расположение корней определяются для ПФ замкнутой системы. Выбор коэффициента усиления автомата устойчивости и демпфирования завершает расчет ядра системы.
Особенности расчета траекторного контура.
ПФ по траекторному параметру может содержать одно-два интегрирующих звена.
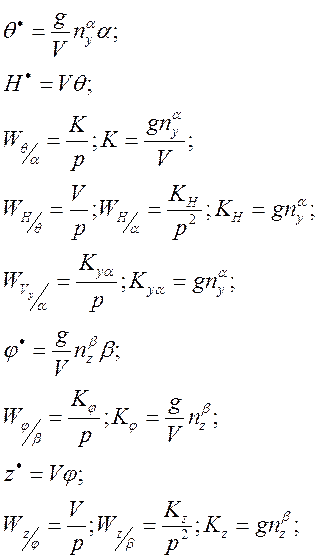
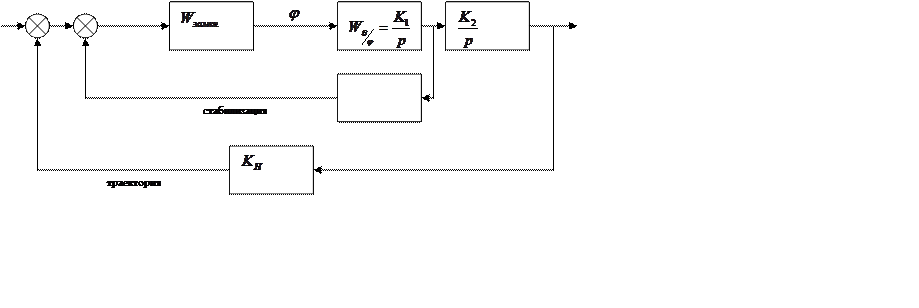 Контур траекторного управления может быть
структурно – неустойчивым и содержать два интегрирующих звена. В этом случае
двойное интегрирующее звено рассматривается как два последовательно соединенных
интегральных звена, каждое из которых охватывает обратной, отрицательной связью
по скорости и величине изменения траекторного параметра и последовательно
вычисляющихся два коэффициента усиления по запасам устойчивости. Для каждого
контура и всей системы проверяют запасы устойчивости и с учетом выбранных
коэффициентов определяется характер переходных процессов и расположение корней
для замкнутых контуров.
Контур траекторного управления может быть
структурно – неустойчивым и содержать два интегрирующих звена. В этом случае
двойное интегрирующее звено рассматривается как два последовательно соединенных
интегральных звена, каждое из которых охватывает обратной, отрицательной связью
по скорости и величине изменения траекторного параметра и последовательно
вычисляющихся два коэффициента усиления по запасам устойчивости. Для каждого
контура и всей системы проверяют запасы устойчивости и с учетом выбранных
коэффициентов определяется характер переходных процессов и расположение корней
для замкнутых контуров.
Задание по первому этапу выполнения курсовой работы:
1)Определить ПФ всех элементов САУ и по заданному режиму указать значения коэффициентов усиления постоянной времени и относительного коэффициента демпфирования.
2)По методичке(Гуськов, Загайнов «Управление полетом самолета»)составить полную математическую модель и линеаризованное уравнение движения самолета, определить ПФ по различным параметрам движения.
Исследование СУ с учетом нелинейных элементов.
Нелинейный элемент определяет соотношение между входной и выходной координатой в виде нелинейных функций.
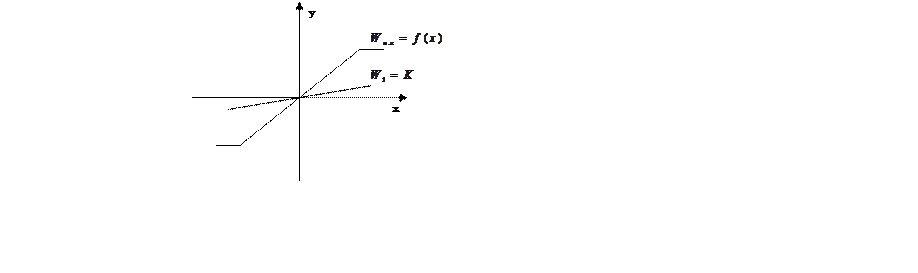
Анализ нелинейных систем СУ включает изучение следующих типов нелинейностей:
1)Типовые нелинейности СУ
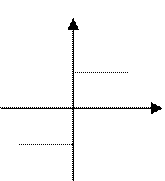 Идеальное реле
Идеальное реле
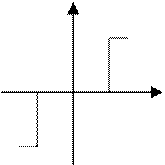 Реле с зоной нечувствительности
Реле с зоной нечувствительности
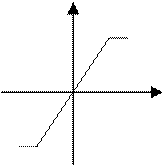 Реле с ограничением
Реле с ограничением
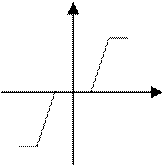 Реле с зоной нечувствительности и с ограничением
Реле с зоной нечувствительности и с ограничением
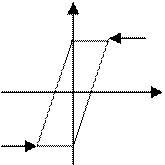 Гистерезис
Гистерезис
2)Нелинейные ДУ объектов управления и элементов САУ
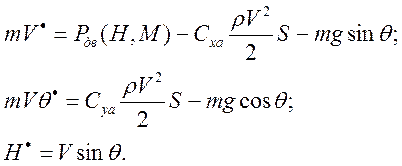
Нелинейность ДУ является следствием нелинейных функций и нелинейных операций умножения/деления координат объекта управления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.