Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления, страница 16

внутри которой сохраняется условие устойчивости и близость динамических характеристик. Т.е. при отклонении фазовых координат менее допустимых значений на интервале времени t, отклонения координат не превысят величины .

Теорема Ляпунова:

1) Если линеаризованная система ДУ является устойчивой, то и нелинейная система является устойчивой в –окрестности.

2) Если линеаризованная система ДУ является неустойчивой или нейтральной в окрестности опорной траектории, то и нелинейная система является устойчивой.

3) Линеаризованная система называется асимптотически-устойчивой в –окрестности опорной траектории, если при выполнении неравенства:

Для линеаризованной системы при заданных характеристиках нелинейной системы можно указать следующие области:

1) –окрестность, внутри которой соблюдается условие устойчивости нелинейной системы при устойчивости линеаризованной модели и совпадают их характеристики во временной области с заданной точностью.

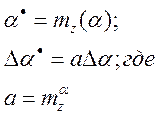
Если -линеаризованная модель устойчива и нелинейная модель устойчива.

Ошибкой линеаризации () называется разность вычислений:

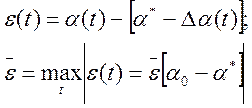
Погрешность линеаризации зависит от начального отклонения вектора координат от опорного (расчетного) значения.

2) Областью устойчивости нелинейной системы называют область значений фазовых координат, внутри которой нелинейная и линеаризованная система являются устойчивыми, но временные характеристики существенно различаются.

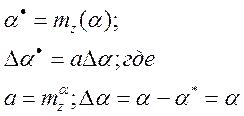
Методы исследования устойчивости нелинейной системы по линеаризованным моделям.

Исследование устойчивости нелинейной системы включает определение следующих факторов:

1) расчет балансировочного значения нелинейных координат.

Эта задача решается методом расчета корней системы нелинейных алгебраических уравнений

Дано:

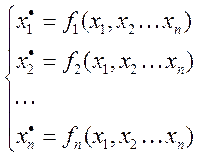
Требуется определить:

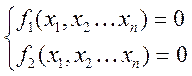
При значении координат системы, соответствующих корням нелинейного уравнения, динамическая система находится в положении равновесия. Для всех положений равновесия ставится задача исследования на устойчивость.

2) Для опорных режимов полета, соответствующих положению  равновесия, требуется определить устойчивость нелинейной системы в –окрестности.

Данная задача решается на основе замены нелинейной модели линеаризованной и определение устойчивости линеаризованной математической модели методом корней характеристического уравнения Раусса-Гурвица по коэффициентам полинома или по устойчивости передаточной функции динамической системы.

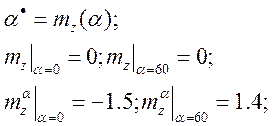
динамический коэффициент

характеристическое уравнение

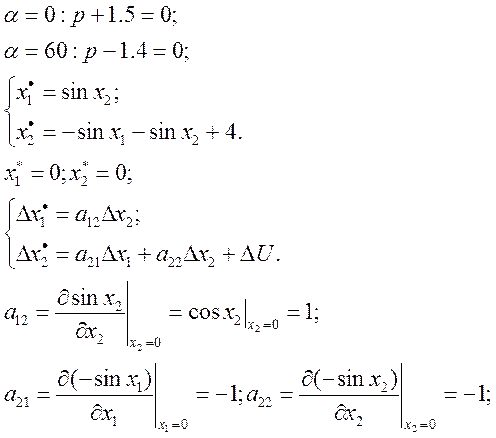
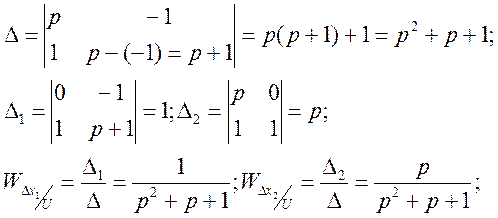
Рассмотрим определение передаточной функции для нелинейной динамической системы следующего вида:

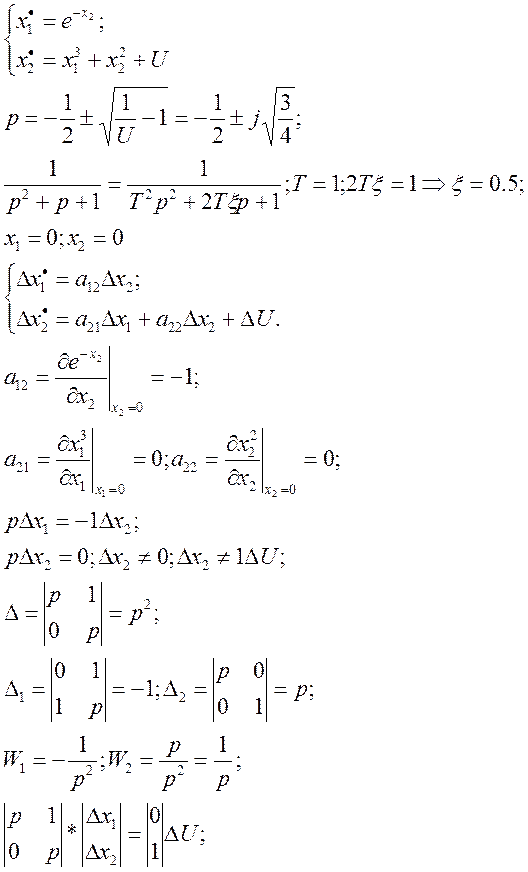
Передаточные функции по отклонению 1-ой и 2-ой координат   и    содержат нулевой полюс p=0 линеаризованная система находится на границе устойчивости и нелинейная система не будет обладать устойчивостью.

Для исследования свойств передаточных функций линеаризованных систем могут быть использованы стандартные программы MatLab для расчета карты нулей и полюсов, запасов устойчивости по амплитуде и фазе диаграммы Bode (ЛАФЧХ). Об устойчивости можно судить по реакции на ступенчатый сигнал, импульсное воздействие и по годографу передаточной функции.

Методы исследования нелинейных динамиченских систем и линеаризованных моделей.

Синтез нелинейной системы управления представляет собой решение задачи о выборе управления нелинейной системой в целях обеспечения устойчивости и заданных динамических свойств (времени регулирования, относительного коэффициента перерегулирования и времени срабатывания).

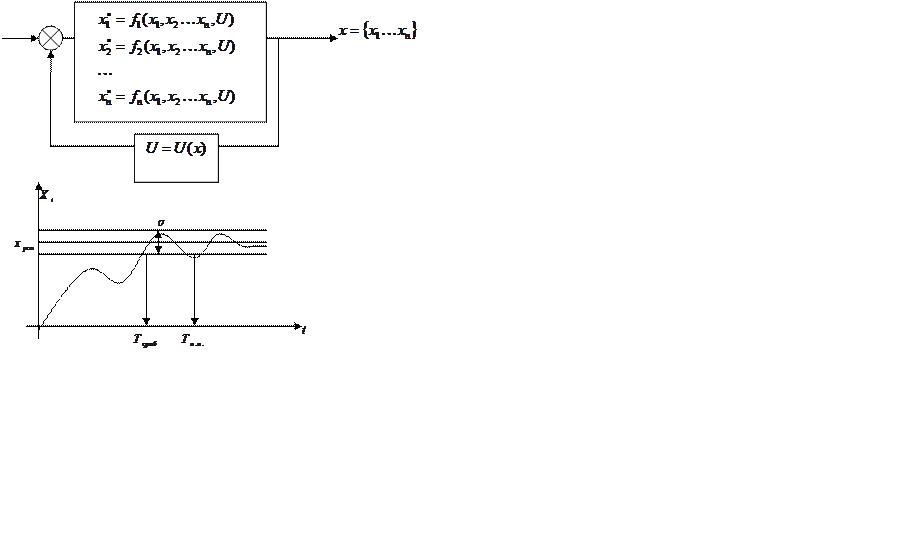
Для синтеза управления технической системой используют линеаризованную математическую модель.

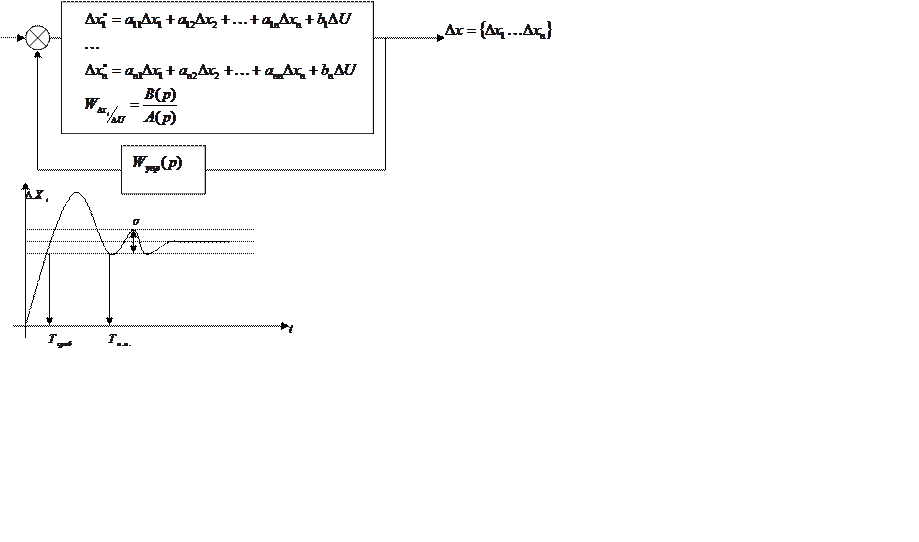
Для выбора алгоритма управления:

Или передаточную функцию автоматического устройства

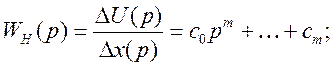
Для выбора коэффициента настройки автопилота  используют метод расчета желаемой передаточной функции замкнутой системы при аналитическом решении, либо желаемой передаточной функции разомкнутой системы методом наращивания устойчивых контуров или другие подходы.