Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления, страница 22

В случае численного расчета производится алгоритм работы БЦВМ существенно изменяются:

-алгебраическая функция

Измеряется только x:

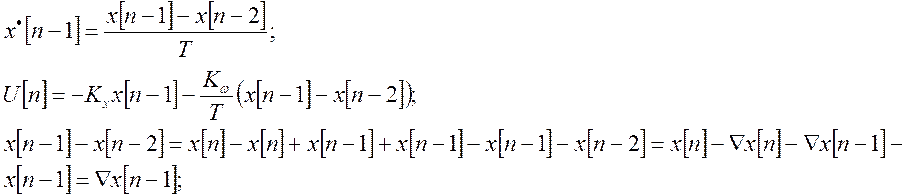
-для БЦВМ, где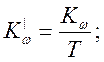

Выводы:

Таким образом при использовании БЦВМ в системе управления необходимо в памяти компьютера сохранять значения решетчатой функции на предыдущих шагах в зависимости от используемого алгоритма.

Алгоритм расчета БЦВМ при использовании д.у:

Алгоритм управления по д.у. используется для вариантов решения управления в интегро-дифференцированной форме и в случае управления по эталонной модели.

-оптимальный алгоритм управления

Требуется разработать дискретный алгоритм:

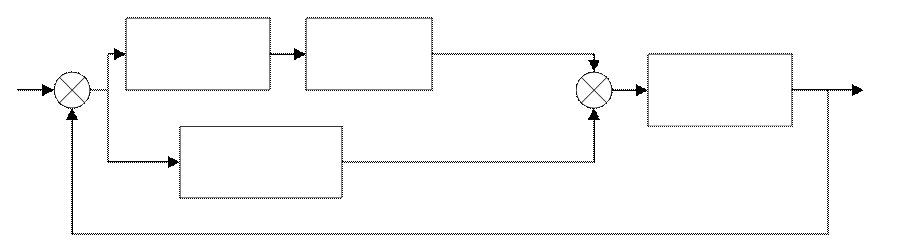
В случае управления по эталонной модели и по настраиваемым параметрам ставится задача расчета желаемого изменения координат:

Для сравнения с реальным поведением объекта в целях коррекции его пилотажных характеристик, таким образом в оптимальных и адаптивных системах управления необходимых БЦВМ разработать дискретный  алгоритм для интегрирования системы ДУ, управления или эталонного объекта.

В качестве методов решения используются метод фундаментальных решений и метод конечных разностей.      

Алгоритмы решения д.у. БЦВМ

Д.у. в БЦВМ решается в дискретной форме. Для решения используются фундаментальные решения д.у. и конечно-разностные методы решения д.у.

1) фундаментальные решения л.д.у.

Исходными данными являются д.у. n-ой степени:

Дано:

  

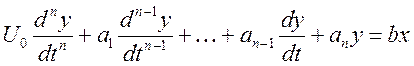
Решение уравнения включает общее и частное решения.

   

Общее решение:  

-корни характеристического уравнения

-коэффициенты, либо собственный вектор

Для определения частного решения необходимо задать структуру функций для описания управления:

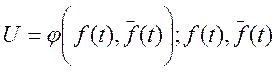-сопряженные функции

        

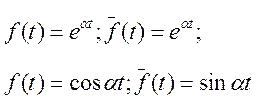
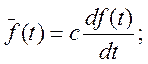
Частное решение: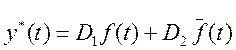

 Фундаментальное решение системы д.у. или д.у. n-го порядка описывает изменение выходной  координаты в виде.

Пример:

при;

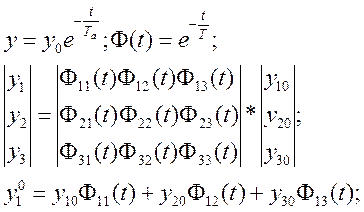
В случае исследования вынужденного движения определяется переходная функция, которая представляет собой изменение координаты при нулевом начальном значении на заданное воздействие.

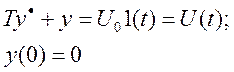
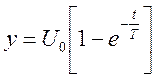-переходная функция;

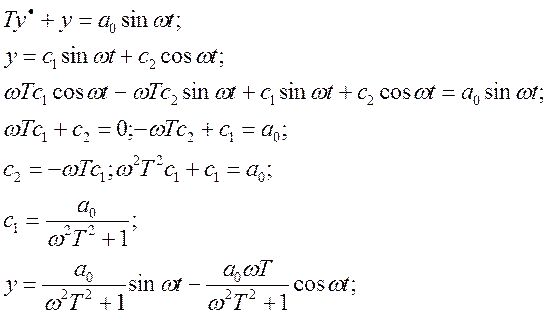
Поиск фундаментального решения и переходных функций позволяет найти точное аналитическое решение д.у. n-го порядка или системы д.у. в виде

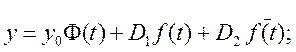
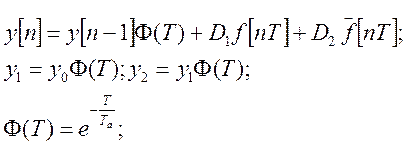
Конечно-разностный метод.

Метод конечных разностей использует расчет приращения функций на шаге дискретности  замену приращений на значения функции в узловых точках.

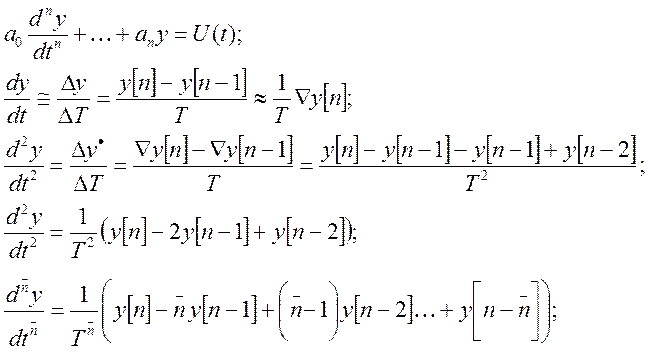
Исходное д.у. заменяется приближенной конечно-разностной формой.

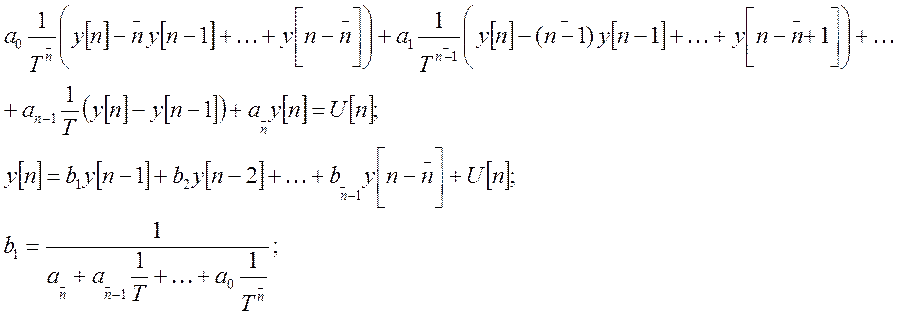
В случае использования метода конечных разностей для одного, либо системы д.у. порядка n. Необходимо в памяти БЦВМ хранить результаты измерения выходной координаты на n-шагах. В случае использования фундаментальных решений в памяти хранится только предыдущее значение и значение фундаментальной матрицы на шаге дискретности.

Статические и динамические характеристики системы управления.

Рассмотрим управление ЛА с цифровой системой управления в обратной связи.

В качестве примера рассмотрим управление углом тангажа самолета Ту-204.

Ставится задача определения математической модели АЦП, вычислителя и ЦАП в части определения их статических и динамических характеристик и уравнений преобразования управляющих сигналов.

1) АЦП

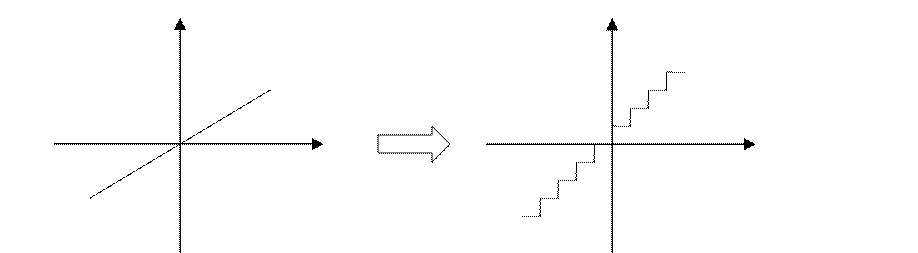
2) ЦАП

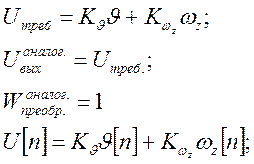
было:

ЦАП позволяет преобразовать дискретный набор значений функции в непрерывный сигнал на каждом интервале. Такие преобразования называются экстраполяцией, а устройство экстраполяции по заданному закону экстраполятору.

1) ступенчатая экстраполяция

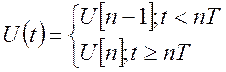
2) экстраполяция звеном 1-го порядка

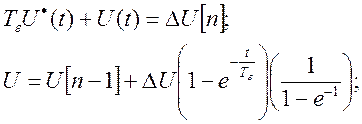
3) экстраполятор на основе линейной установившейся системы 2-го порядка

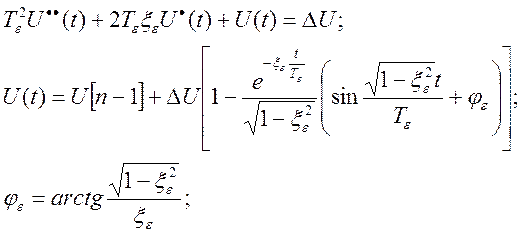
Использование экстраполяторов 1-го и 2-го порядка позволяет преобразовать дискретные команды управления в непрерывный закон, который описывается функцией времени в виде экспоненты и гармонического сигнала. Во всех случаях имеет место запаздывание по выработке команды на интервал дискретности T, связанное с запаздыванием информации. Кроме этого, переход от предыдущего значения команды управления к последующему зависит от инерционности уравнений экстраполятора.

4) экстраполятор нулевого порядка

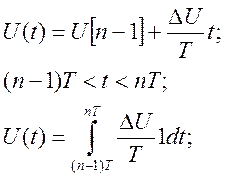
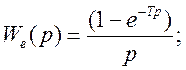
Передаточные функции экстраполяторов.