Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

	ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) « МАИ »

ФАКУЛЬТЕТ  N 1

КАФЕДРА  106

Маркин Н.Н.

Управление в технических системах

Конспект лекций

М о с к в а

2007

Введение.

Любая техническая система описывается замкнутой структурной схемой. Элементами этой схемы являются:

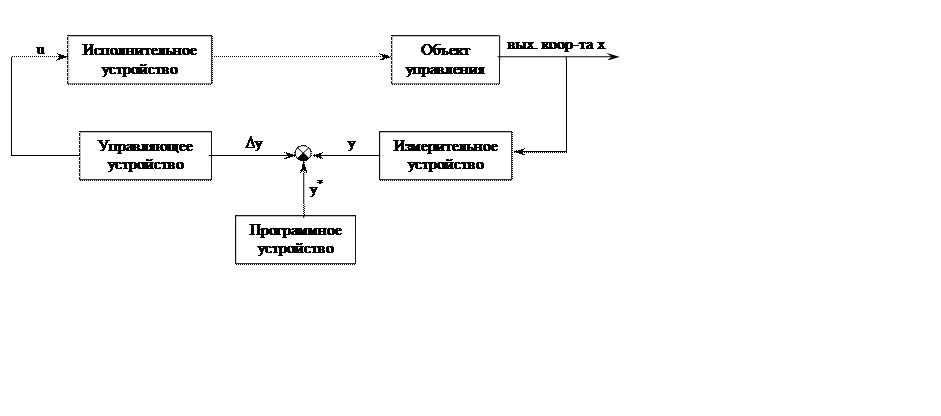
Теория автоматического управления изучает решение следующих задач:

·  определение статических и динамических характеристик элементов системы управления;

·  исследование свойств элементов технической системы в частотной и временной области;

·  анализ структурных схем управления объектом и определение устойчивости, частотных и временных характеристик для разомкнутой и замкнутой системы;

·  синтез алгоритмов управляющих и корректирующих устройств для выполнения заданных технических требований;

·  исследование влияния нелинейных и дискретных элементов системы на режимы автоколебания и запасы устойчивости.

Для решения перечисленных задач в теории автоматического управления рассматриваются следующие разделы:

·  линейный анализ систем управления;

·  синтез линейных систем управления;

·  исследование динамики линейной системы с нелинейными и дискретными элементами в цепи обратной связи.

Линейный анализ систем управления.

В данном разделе рассматриваются элементы систем управления, которые обладают следующими свойствами:

1.  Статические характеристики линейных элементов описываются линейной зависимостью;

2.  Динамика движения линейного элемента описывается линейными дифференциальными уравнениями;

3.  Структура технической системы, которая включает объект управления, измерительные и управляющие устройства, включает только линейные элементы.

Статические свойства: , но соотношение между ними будет описываться некоторой статической характеристикой:

, где  – коэффициент усиления.

Динамические свойства:

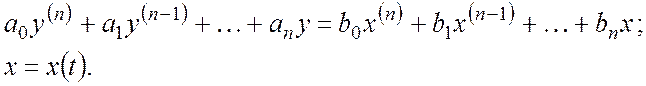
Это дифференциальное уравнение порядка  можно преобразовать к форме Коши:

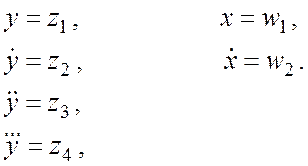
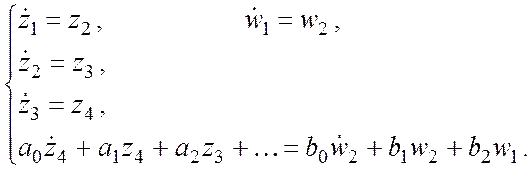
Исследование элементов линейной системы управления.

Для исследования линейных систем управления используются методы решения линейных дифференциальных уравнений, операторные и частотные методы.

Для исследования линейной системы необходимо составить дифференциальные уравнения на основе методов физики и теоретической механики и выполнить их преобразование операторными, частотными методами и найти решение дифференциальных уравнений.

1.  Разработка математической модели:

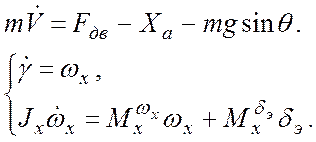
Уравнения разрешаются относительно входного и выходного сигналов в правой и левой части.

2.  Преобразование:

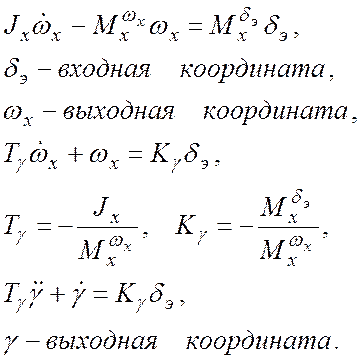
3.  Оператор Лапласа, операторная форма записи дифференциального уравнения и передаточная функция:

Лаплас ввел оператор преобразования .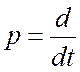

Операторная форма записи дифференциального уравнения:

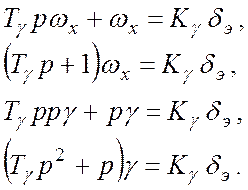
Передаточная функцияпредставляет собой отношение изображения координаты на выходе к входной координате.

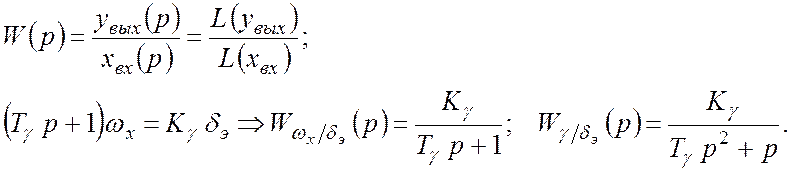
Примеры решения задач по определению передаточной функции.

Пример 1:

Дано:

Определить:

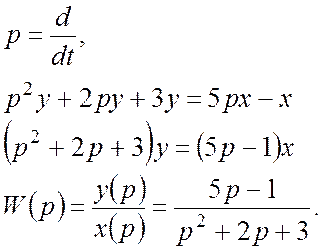
Пример 2:

Дано:

Определить:

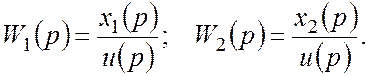
Операторная форма уравнений:

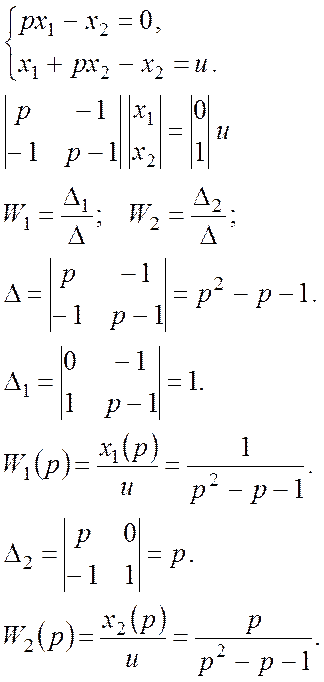
Пример 3:

Дано:

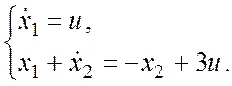
Определить:

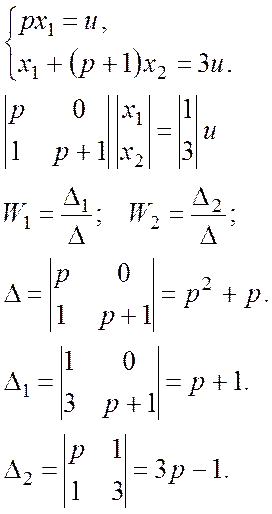
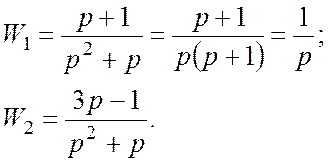
4.  Гармонический анализ элементов систем управления. Преобразование Фурье. Логарифмические амплитудные и фазовые частотные характеристики.

Гармонический анализ исследует характеристики колебаний на выходе элемента систем управления, либо на выходе технической системы в целом в зависимости от частоты гармонического сигнала на входе.

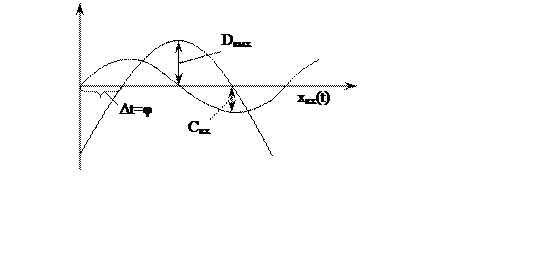
Для устойчивых элементов системы управления на выходе формируется гармоническое колебание с той же частотой, но с другой амплитудой и сдвинутая по фазе.

Амплитудной характеристикой линейной системы называется соотношение амплитуд колебаний на выходе и на входе.

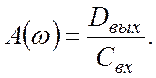
Фазовая характеристика представляет собой разность фаз колебаний сигнала на выходе и на входе.

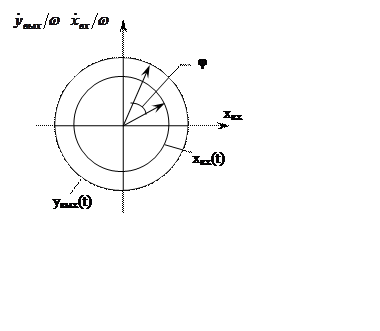
На фазовой плоскости годографы входного и выходного сигнала описывают окружности разного диаметра.

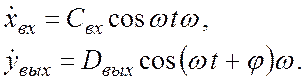
На практике для определения амплитудной и фазовой частотной характеристик используют генератор частоты, и характеристики по времени входного и выходного сигналов регистрируются осциллографом.

Соотношение радиусов окружностей сигнала на выходе к входу определяют амплитудную характеристику, а фазовое запаздывание сигнала на выходе по отношению к входному – фазовую характеристику.

Для вычисления частотных характеристик используется оператор Фурье, который связан с оператором Лапласа соотношением:

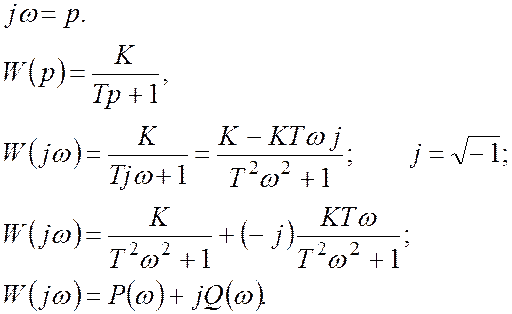
где  – вещественная часть передаточной функции,

 – мнимая часть передаточной функции.

ω	P	Q
ω1	P1	Q1
ω2	P2	Q2
ω3	P3	Q3