Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления, страница 4

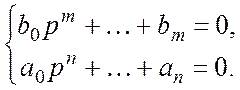
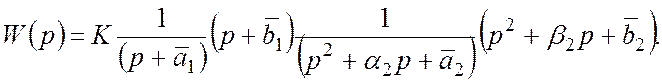
Каждый отдельный полином или его обратная величина представляют собой элементарные звенья систем управления.

Ставится задача изучить характеристики элементарных звеньев и по этим характеристикам определить свойства передаточной функции всей системы .

1.  Усилительное звено.

Уравнение:

Преобразование Лапласа:

Передаточная функция:

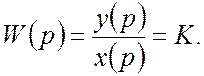
Преобразование Фурье:

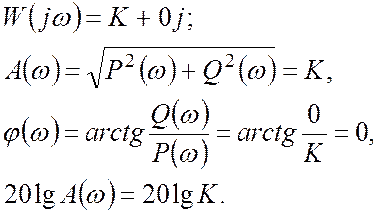
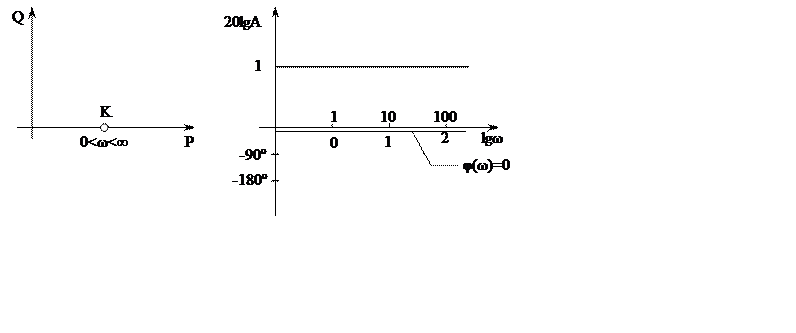
Примерами усилительных звеньев является штурвал самолета, механизм поворота руля высоты, руля направления или элеронов, зубчатые передачи и аналогичные устройства.

2.  Форсирующее звено первого порядка.

Уравнение:

Преобразование Лапласа:

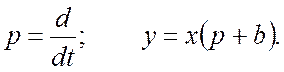
Передаточная функция:

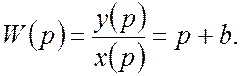
Преобразование Фурье:

Частотные характеристики:

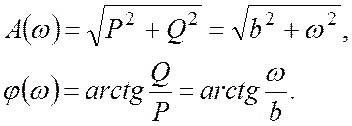
Логарифмические характеристики:

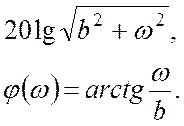
Примерами форсирующих звеньев являются электродвигатели, гидроусилители и (R–C) цепочки с форсирующими свойствами.

3.  Апериодическое звено.

Уравнение:

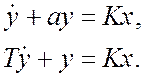
Примерами апериодических звеньев являются объекты с инерционными свойствами в угловом, либо линейном движении.

Движение крена:

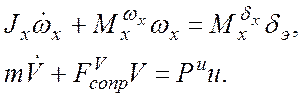
Преобразование Лапласа:

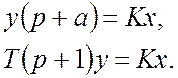
Характеристическое уравнение:

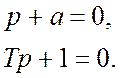      Корни: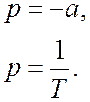 

Решение дифференциального уравнения:

–общее решение.

Частное решение при  при :

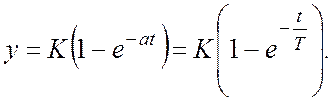
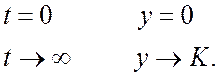
Передаточная функция апериодического звена определяется значением коэффициента усиления и постоянной времени.

Передаточная функция:

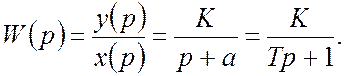
Время переходного процесса и время срабатывания для апериодического звена совпадают и равны утроенному значению постоянной времени.

Преобразование Фурье:

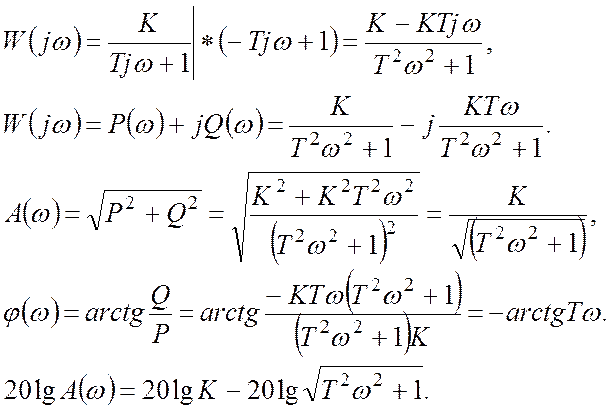
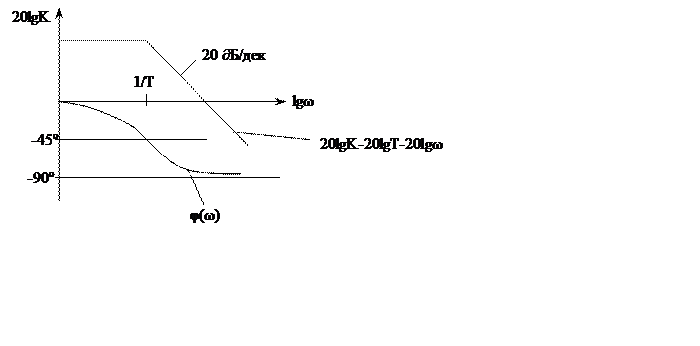
4.  Форсирующее звено второго порядка.

Форсирующее звено второго порядка используют для управления процессом. Существует три значения о характеристиках входной переменной.

·  значение координаты;

·  значение скорости изменения координаты;

·  значение ускорения об изменении координаты.

где  – коэффициент усиления;

 – постоянная времени;

 – коэффициент относительного демпфирования.

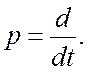
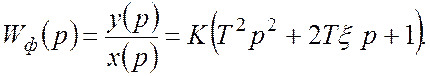
Частотные характеристики:

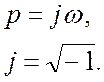
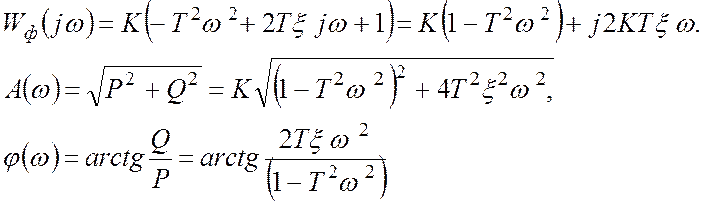
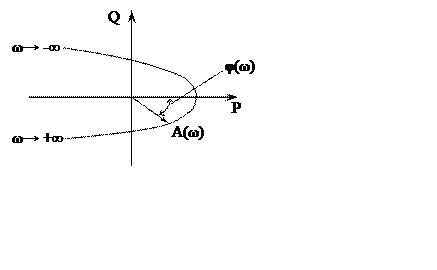
Логарифмические амплитудно-фазовые частотные характеристики:

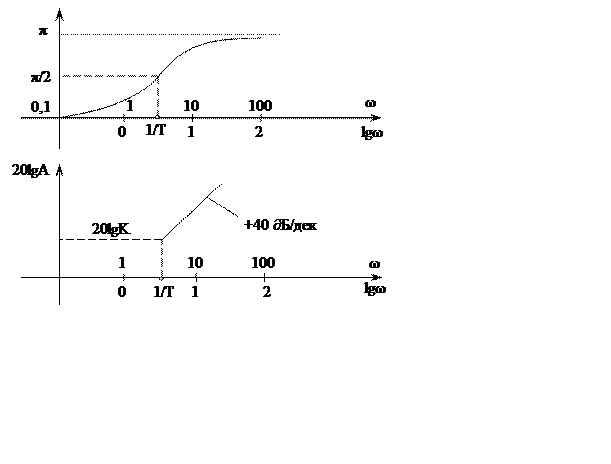
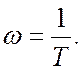
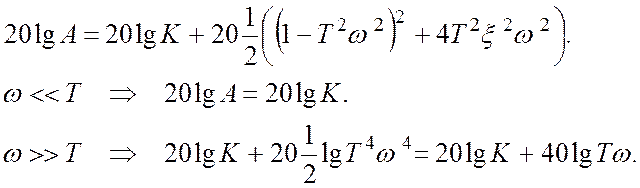
Форсирующее звено второго порядка позволяет на больших частотах увеличить значение фазового сдвига до величины +180º.

Амплитудная характеристика изменяет свой наклон на больших частотах на величину +40 ∂Б/дек.

5.  Колебательное звено.

Колебательное звено представляет собой инерционное звено второго порядка, движение которого в случае устойчивости сопровождается созданием статического усилия по отклонению, направленного к положению равновесия, и демпфирующего усилия, препятствующего движению.

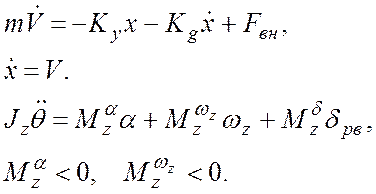
Движение инерционной системы второго порядка описывается уравнением колебательного звена в одной из следующих форм:

·  ;

·  .

В этих уравнениях  – коэффициент усиления,  – постоянная времени, 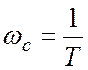 – частота собственных колебаний колебательного звена,  – коэффициент относительного демпфирования.

Характеристическое уравнение:

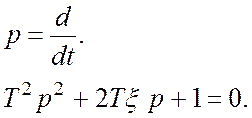
Корни:

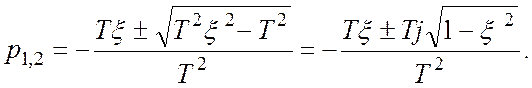
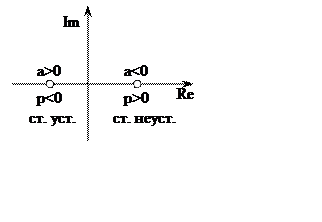
У устойчивого колебательного звена корни комплексные, сопряженные с отрицательной вещественной частью.

Передаточная функция:

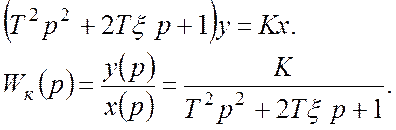
Частотные характеристики:

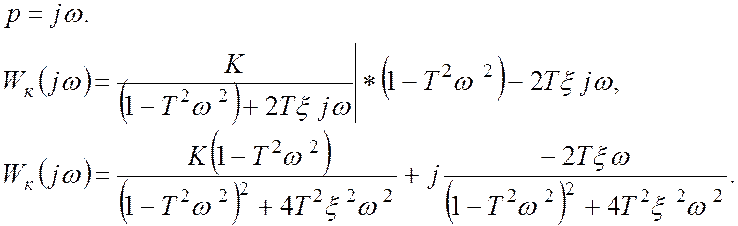
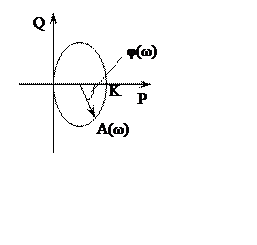
Характеристики колебательного звена.

Уравнение колебательного звена:

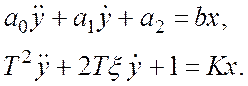
Передаточная функция:

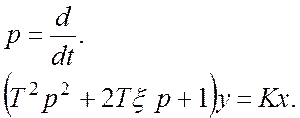
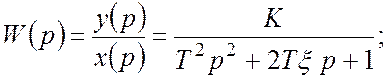
Характеристическое уравнение:

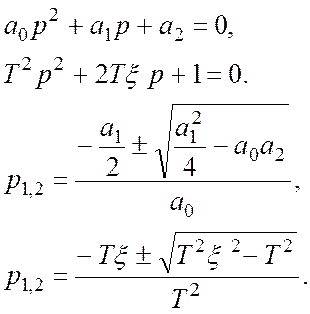
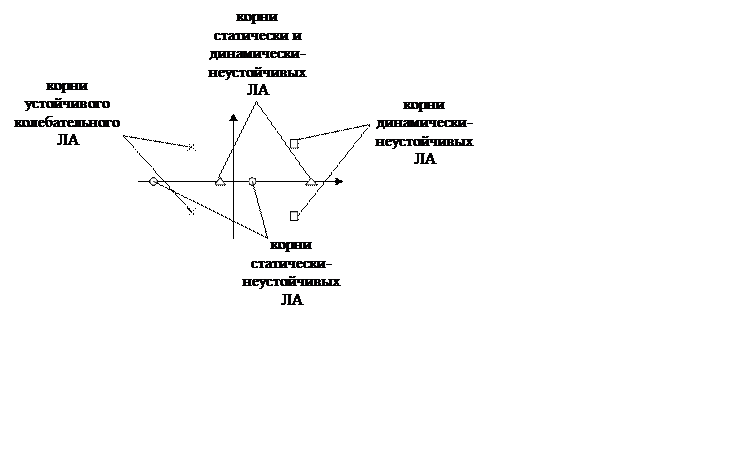
Для статически–неустойчивых ЛА

Для динамически–неустойчивых ЛА

Для статически и динамически–неустойчивых ЛА

Переходный процесс:

\

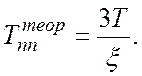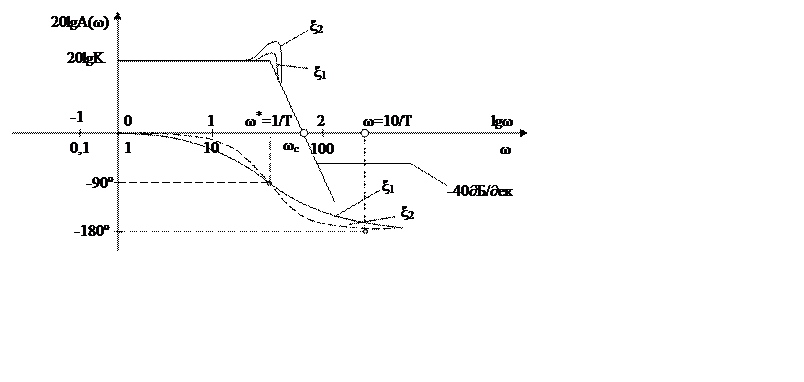
Частотные характеристики:

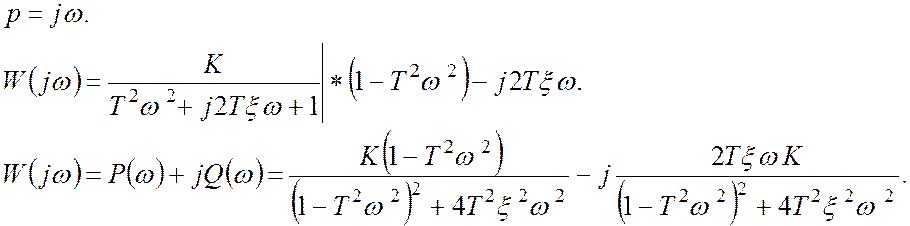
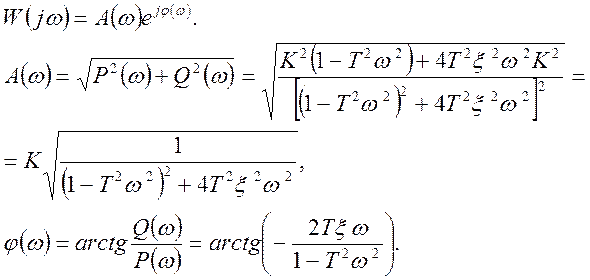
Логарифмическая амплитудная характеристика:

Асимптоты:

· 

· 

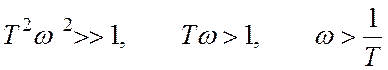
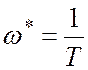 называется собственной частотой колебаний технической системы или резонансной частотой.

Амплитудная характеристика на резонансной частота возрастает. Увеличение амплитуды на резонансной частоте тем больше, чем меньше коэффициент демпфирования.

Значение частоты, при которой амплитудная характеристика пересекает ось частот, называется частотой среза или максимальной частотой пропускания системы.