
В случае линейной части с передаточной функцией колебательного звена замкнутой системы с отрицательной обратной связью и нелинейностью в цепи обратной связи сохраняет устойчивость.
Условие устойчивости соблюдается и для класса функций с бесконечным коэффициентом усиления.
Годограф Найквиста:

Рассмотрим передаточную функцию более высокого порядка:
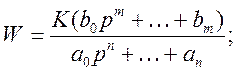

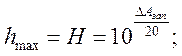
Для линейной системы выше 2-го порядка ставится задача определения max коэффициента усиления H в цепи обратной связи для обеспечения устойчивости замкнутой системы. Если решение задачи существует, то max коэффициент усиления H определяющий класс нелинейного элемента, гарантирует устойчивость замкнутой системы.
Устойчивость динамической системы с нелинейным элементом в цепи обратной связи.
Рассмотрим динамическую систему, описываемую следующей структурной схемой:
|
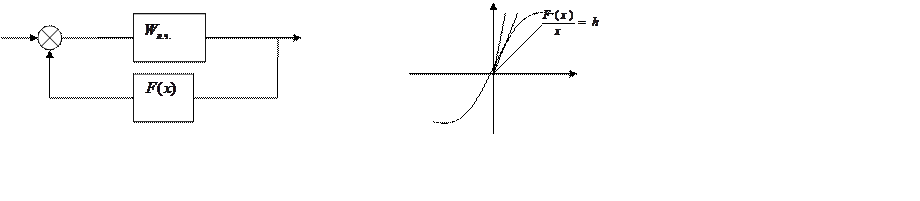
Нелинейная функция относится к классу однозначных характеристик с ограниченными значениями секущей и касательной, проведенные из начала координат.
![]()
Требуется определить расположение годографа линейной части на комплексной плоскости, обеспечивающая устойчивость замкнутой системы с нелинейной характеристикой заданного класса.
Рассмотрим передаточную функцию замкнутой системы при max значении коэффициента усиления нелинейного элемента в цепи обратной связи.
|

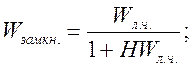
Условие устойчивости:
![]() если
если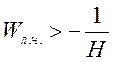
![]()
Нелинейная система с
нелинейным коэффициентом класса H в цепи обратной связи будет обладать устойчивостью,
если годограф передаточной функции линейной части не охватывает точку с
координатами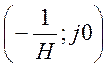 расстояние по вещественной оси от
критической точки до годографа представляет собой запас устойчивости по
амплитуде, а угол поворота критической точки относительно начала координат до
годографа представляет собой запас устойчивости по фазе.
расстояние по вещественной оси от
критической точки до годографа представляет собой запас устойчивости по
амплитуде, а угол поворота критической точки относительно начала координат до
годографа представляет собой запас устойчивости по фазе.
Критерий устойчивости Попова для нелинейной системы общего вида.
Теорема Попова определяет условие абсолютной устойчивости динамических систем с линейной частью и нелинейными элементами класса H в цепи обратной связи.
Рассматривается структурная система динамической системы замкнутого типа:
|

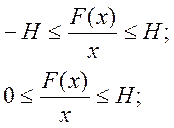
Частным случаем является
условие, что![]() .
.
Теорема Попова определяет
условие абсолютной устойчивости для линейной системы с произвольной нелинейной
функцией из подкласса![]() в цепи обратной связи.
в цепи обратной связи.
1) Рассмотрим случай нелинейной функции F(x), удовлетворяющей следующим условиям:
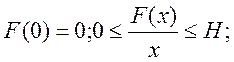
Для оценки устойчивости Попов
предложил вычислить годограф функции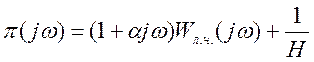 .
.
Теорема абсолютной устойчивости Попова:
Если существует такое число![]() , при котором вещественная часть функции
Попова всегда положительна при любой частоте, то замкнутая система обладает
устойчивостью с любой нелинейной функцией заданного класса H.
, при котором вещественная часть функции
Попова всегда положительна при любой частоте, то замкнутая система обладает
устойчивостью с любой нелинейной функцией заданного класса H.
Геометрическая интерпретация:
Запишем годограф линейной части:
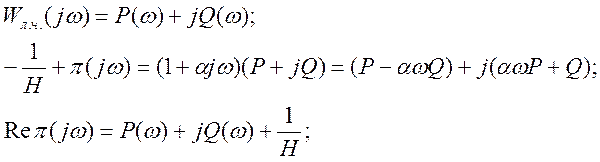
Введем преобразованную передаточную функцию:
![]() где
где![]()
Вещественная и мнимая части представляют собой четные функции частоты. Для положительной определенности вещественной части функции Попова должны выполняться следующие условия:
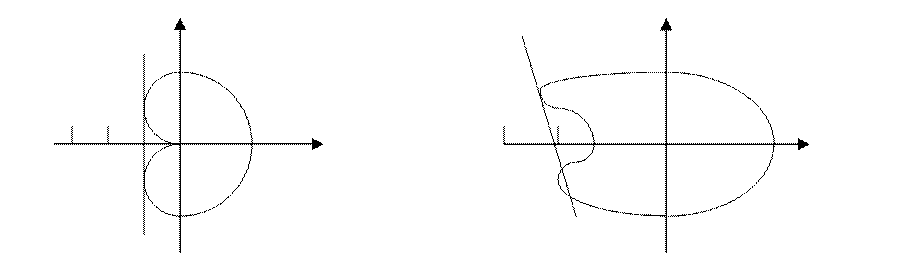
устойчивая замкнутая система замкнутая неустойчивая система
с нелинейным элементом класса H
Линейная система с
произвольной нелинейной функцией класса H в цепи
обратной связи будет устойчива, если из критической точки с координатой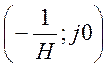 можно провести касательную с тангенсом угла
можно провести касательную с тангенсом угла![]() , которая не будет пересекать годограф
преобразованной передаточной функции с вещественной частью
, которая не будет пересекать годограф
преобразованной передаточной функции с вещественной частью![]() и мнимой
и мнимой![]() .
.
Рассмотрим годограф передаточной преобразованной функции аналогичный апериодическому звену:
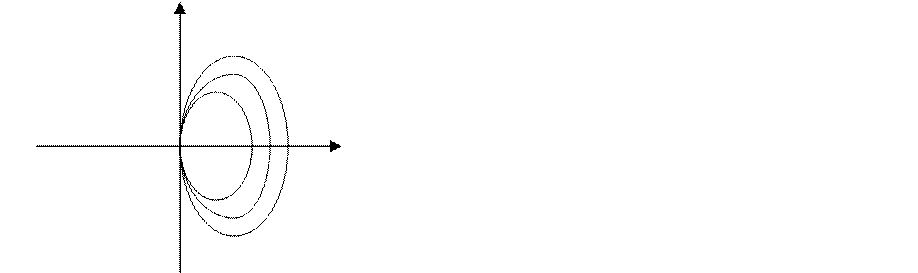
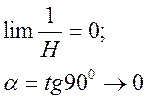
Теорема Попова для линейной системы, устойчивой в замкнутом состоянии:
В этом случае коэффициент
усиления в цепи обратной связи ограничен допустимым min и max
коэффициентом усиления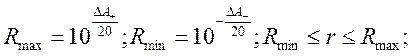
Для устойчивости замкнутой системы неустойчивой в разомкнутом состоянии нелинейная функция в цепи обратной связи должна обладать следующими свойствами:
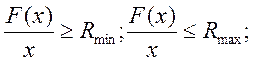
Функция Попова![]() для неустановившейся системы:
для неустановившейся системы: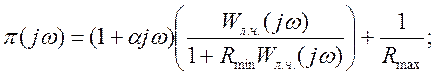
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.