Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления, страница 7

 – матрицы динамических коэффициентов (матрицы координат и управления).

Рассматривается состояние равновесия линейной динамической системы в начальный момент времени.

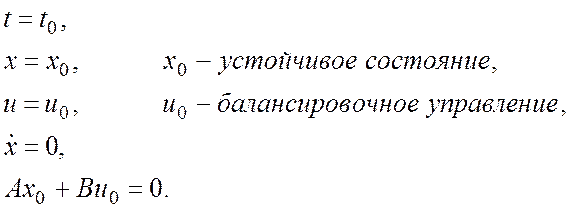
Понятие управляемости для автоматических систем интерпретирует следующее свойство: линейная динамическая система называется управляемой, если на интервале  можно указать такое управляющее воздействие , которое переводит линейную систему в состояние .

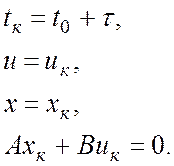
По теореме Ляпунова необходимо, чтобы при любом заданном изменении  существовала такая величина , чтобы выполнялись условия:

при

Интерпретация для технических систем.

Рассматривается реакция динамической системы на ступенчатое управляющее воздействие. Требуется, чтобы за время срабатывания  или за время переходного процесса  система достигла требуемого фазового состояния .

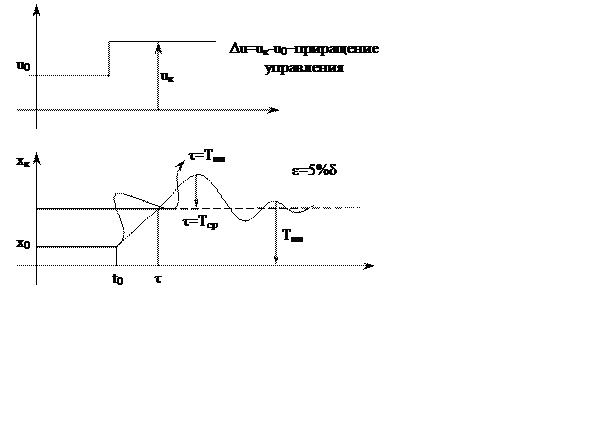
В техническом приложении допустимое отклонение  составляет 5% от величины изменения фазовой координаты за время переходного процесса.

Замечание: Устойчивость по Ляпунову определяется для свободного движения динамической системы при начальном отклонении.

Устойчивость линейной динамической системы при исчезающее–малых импульсных воздействиях и управляющих ступенчатых воздействиях характеризуют вынужденное движение при внешних воздействиях заданного типа. В этом случае траектория динамической системы определяется как сумма общего решения дифференциального уравнения и частного решения.

Статические и динамические системы.

Рассмотрим поведение устойчивой линейной системы при внешнем воздействии .

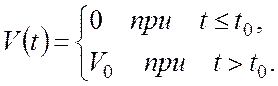
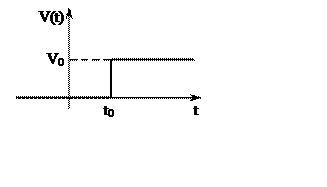
Рассмотрим изменение одной из координат  для линейной динамической системы.

Определение статической системы:

Линейная система называется статической по координате , если при воздействии  установившееся значение координаты будет равно .

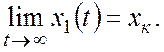
Коэффициент усиления для статической системы определяется соотношением:

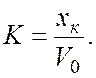
Определение астатической системы:

Линейная динамическая система называется астатической, если для любого внешнего воздействия

Техническое приложение.

1.  Для автоматических систем управления требуется, чтобы линейная система была статической по отношению к управляющим воздействиям:

2.  По отношению к возмущающим воздействиям требуется, чтобы динамическая система была астатической, либо при максимальном возмущающем воздействии отклонение не выходило за требуемые значения по точности.

Астатическая система: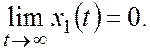

Статическая система: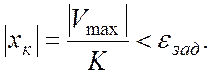

Исследование устойчивости динамической системы по значениям корней характеристического уравнения.

Определение устойчивости системы по значениям корней характеристического уравнения позволяет судить о движении по изменению координат.

Рассмотрим дифференциальное уравнение n-го порядка:

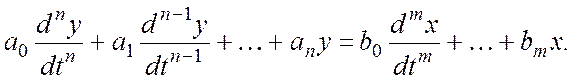
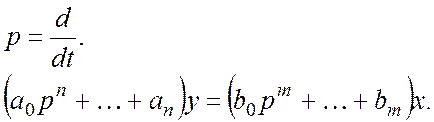
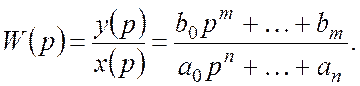
Для данной передаточной функции обычно рассматриваются два характеристических уравнения для расчета нулей и полюсов системы:

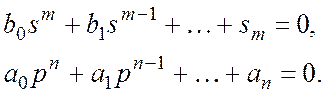
–нули динамической системы,

–полюса динамической системы,

Для оценки устойчивости определяющее значение имеют значения полюсов системы и соответствующее характеристическое уравнение. Расположение нулей влияет на запасы устойчивости, но не влияет качественно на устойчивость.

В общем случае значения корней характеристического уравнения

могут быть как вещественными, так и мнимыми:

Рассмотрим в качестве нормативного показателя значения частоты :

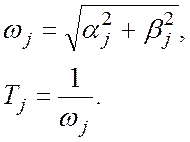
Такой подход определяется следующим представлением характеристического уравнения:

Для сопряженных корней можно получить следующее уравнение:

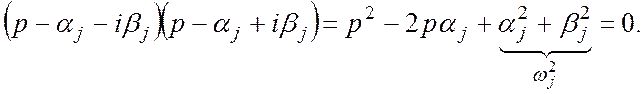
Для решения технических задач производят ранжирование коней характеристического уравнения по значению обобщенного показателя .

В порядке возрастания  или убывания  выделяют первую форму движения, вторую форму движения и последующие формы.

Значения корней характеристического уравнения или собственные значения определяют общее решение дифференциального уравнения.

В силу аддитивности полученного решения для устойчивости динамической системы при начальных отклонениях необходимо, чтобы все вещественные части корней характеристического уравнения были отрицательными.