Если для нелинейной ДС существует положительно определенная функция Ляпунова, производная от которой является отрицательной на области значений фазовых координат, то такая нелинейная ДС будет устойчива.
Если производная функции Ляпунова строго отрицательна, т.е. не имеет нулевых значений, то нелинейная динамическая система будет асимптотически устойчивой.
Геометрическая интерпретация:
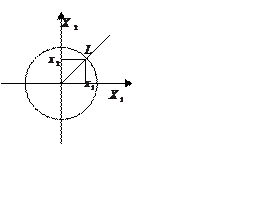 Рассмотрим нелинейную ДС описываемую
двумя фазовыми координатами, определяющие значение функции Ляпунова как квадрат
расстояния до центра системы координат.
Рассмотрим нелинейную ДС описываемую
двумя фазовыми координатами, определяющие значение функции Ляпунова как квадрат
расстояния до центра системы координат.
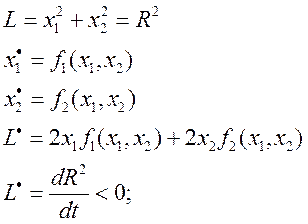
Пример1:
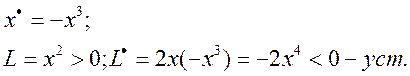
Пример2:
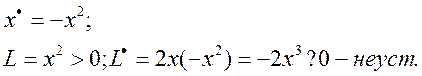
Пример3:
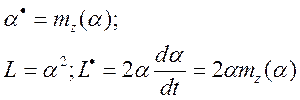
В соответствии с методом
Ляпунова на интервале значений ![]() , где производная
, где производная![]() динамической системы будет устойчива. На
интервале положительно определенная производная функции Ляпунова, динамическая
система будет неустойчивой.
динамической системы будет устойчива. На
интервале положительно определенная производная функции Ляпунова, динамическая
система будет неустойчивой.
Линеаризация нелинейных динамических систем и анализ устой чивости по линеаризованным уравнениям.
Линеаризация представляет собой приближенное описание нелинейной функции линейными многочленами. Для линеаризации необходимо выбрать значения фазовых координат, которые называются опорными, расчетными, базовыми и т.п.
Для линеаризации используют разложение в ряд Тейлора, Лорана и т.п.
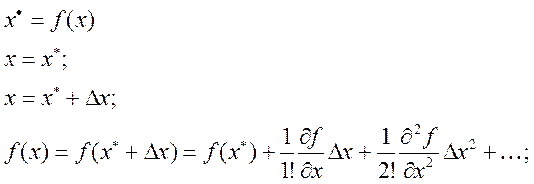
![]() -
линейное приращение координаты;
-
линейное приращение координаты;
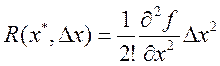 -
остаточный член разложения.
-
остаточный член разложения.
Основные определения:
1)Расчетной или опорной траекторией нелинейной системы называется решение нелинейного ДУ:
2)Линеаризованным ДУ
называется уравнения в приращениях для фазовой координаты ![]() в окрестности опорной траектории
в окрестности опорной траектории
3)Коэффициент 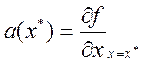 называется коэффициентом линеаризации
называется коэффициентом линеаризации
4)Коэффициенты линеаризации, вычисленные для дифференциальных уравнений сил и моментов, называются динамическими коэффициентами
5)Коэффициенты линеаризации, вычисленные для кинематических уравнений, называются коэффициентами линеаризации кинематических параметров
6)Линеаризованная система называется стационарной, если все коэффициенты линеаризации постоянны и не зависят от времени
Пример линеаризации уравнений прямолинейного уравновешенного движения на постоянной высоте с постоянной скоростью. Еще одним примером является линеаризация бокового движения относительно опорной траектории, движение в Г.П. на постоянной высоте с постоянной скоростью
7)Метод замороженных коэффициентов представляет собой допущения о постоянстве траекторных параметров на малом интервале изменения параметров углового движения.
8)Параметры траекторного движения называются длиннопериодическими. При расчете параметров длиннопериодического движения принимается допущение о балансировке самолета по моментам на каждом режиме.
9)Параметры углового движения обычно рассматриваются как элементарное короткопериодическое движение.
За время переходного процесса изменением координат в длиннопериодическом движении пренебрегают.
Для короткопериодического движения коэффициенты линеаризации рассматриваются как постоянные замороженные значения.
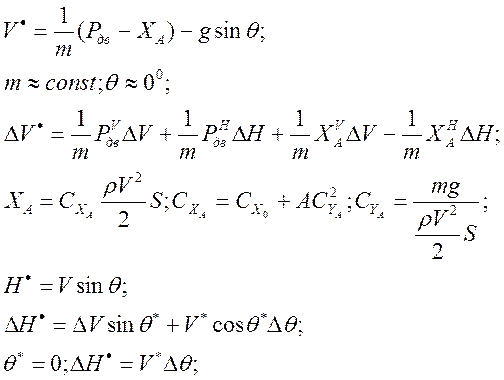
Исследование устойчивости нелинейных динамических систем по линеаризованным моделям
Рассмотрим нелинейную динамическую систему, описываемую ДУ в форме Коши:
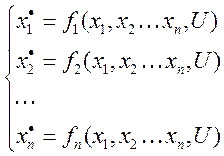
Для данной системы определим балансировочный режим полета по силам и моментам:
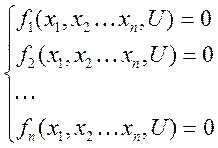
![]() опорный
режим
опорный
режим
Возмущенное движение относительно опорного описывается приращением координат и управления:
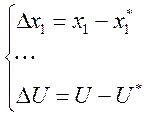
Методом линеаризации определяем уравнение возмущенного движения:
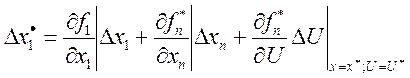
Значения частных производных называются динамическими коэффициентами и линеаризованная система представляет собой следующие математические формы:
1) Система линейных ДУ
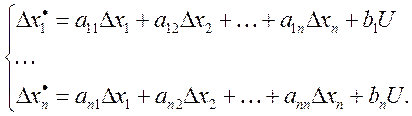
![]()
2) Математическая форма линейной динамической системы
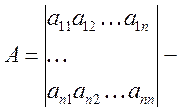 матрица
динамических коэффициентов или матрица коэффициентов линеаризации.
матрица
динамических коэффициентов или матрица коэффициентов линеаризации.
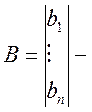 матрица
коэффициентов управления.
матрица
коэффициентов управления.
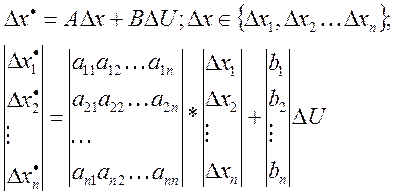
Если A=A(f), то система нестационарная; если A=const, то система стационарная и автономная.
Характеристическим уравнением линеаризованной математической модели называется полином, определяемым значением определителя.
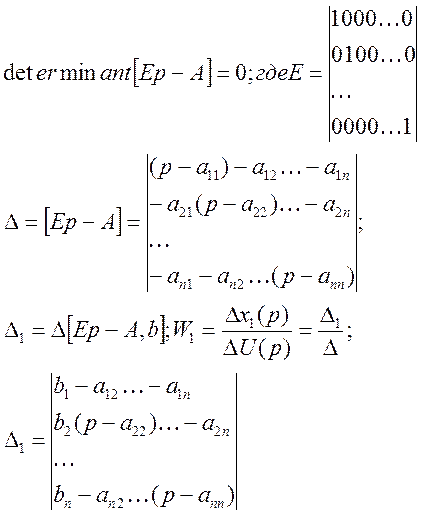
![]() -окрестностью
движения линеаризованной системы относительно опорной траектории называется
такая область допустимых отклонений:
-окрестностью
движения линеаризованной системы относительно опорной траектории называется
такая область допустимых отклонений:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.