![]() однозначная
динамическая нелинейность
однозначная
динамическая нелинейность
![]() неоднозначная
динамическая нелинейность
неоднозначная
динамическая нелинейность
2) передаточная функция нелинейного элемента
Сигнал на выходе y можно представить как результат разложения в ряд Фурье.
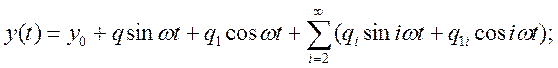
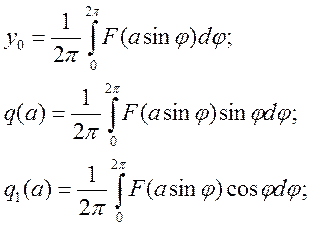 -коэффициенты
ряда Фурье.
-коэффициенты
ряда Фурье.
Т.о. передаточная функция
нелинейного элемента рассматривается как сумма первых членов разложения в ряд
Фурье ![]()
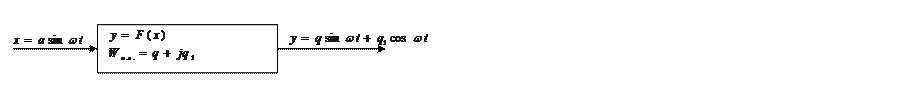

Исследование устойчивости автоколебаний.
Рассмотрим прохождение гармонического сигнала через линейный и нелинейный статический элемент.
![]() на
входе
на
входе
![]() на
выходе
на
выходе
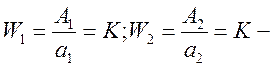 при
линейном сигнале
при
линейном сигнале
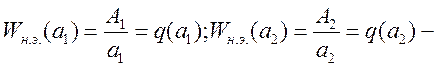 при
нелинейном сигнале
при
нелинейном сигнале
В случае линейной статической характеристики соотношение амплитуд входного и выходного гармонического сигнала равно коэффициенту усиления. Передаточная функция линейного элемента равна коэффициенту усиления и является величиной постоянной.
В случае нелинейной статической характеристики элементы системы управления: отношение амплитуды на входе и выходе зависит от амплитуды входного воздействия. В результате передаточный коэффициент нелинейного элемента q(a) является функцией амплитуды входного воздействия.
Метод Пуанкаре. Определение амплитуды и частоты автоколебаний.
Рассмотрим систему управления с обратной связью:

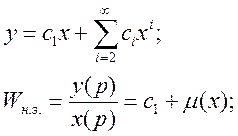
![]() малый
параметр Пуанкаре
малый
параметр Пуанкаре
Рассмотрим случай установившихся автоколебаний с постоянной амплитудой “a”. В этом случае коэффициент усиления нелинейного элемента представляет собой пременную величину, зависящею от амплитуды.
Рассмотрим условие устойчивости динамической системы при различных значениях коэффициентов усиления нелинейных элементов.
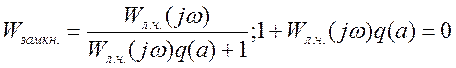
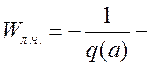 потеря
устойчивости
потеря
устойчивости
Рассмотрим преобразование структурной схемы:



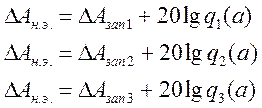
Амплитуда и частота
автоколебаний могут быть определены по ЛАФЧХ. В этом случае необходимым
условием автоколебаний является пересечение фазовой характеристикой уровня в
-180. Максимальная величина приращения логарифмической амплитудной
характеристики равна![]() ;
; ![]() -коэффициент
усиления нелинейного элемента.
-коэффициент
усиления нелинейного элемента.
Передаточная функция нелинейного элемента и определение амплитуды и величины автоколебаний методом гармонического баланса.
Рассмотрим прохождение гармонического сигнала через нелинейный элемент с неоднозначной статической характеристикой.
1) линейная статическая характеристика
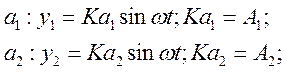 -на
выходе
-на
выходе
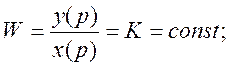
2) нелинейная неоднозначная статическая характеристика
![]() на
выходе
на
выходе
В случае неоднозначной нелинейной статической характеристики происходит изменение формы гармонического сигнала, который с использованием разложения в ряд Фурье рассматривается как сумма 2-х гармоник. Обе гармоники имеют одну и ту же несущую частоту, но сдвинуты по фазе на 90 и могут рассматриваться как наложение колебаний в 2-х плоскостях.

Определение передаточного
числа нелинейного элемента для колебаний по форме ![]() :
: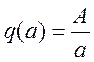 Для колебаний по форме
Для колебаний по форме![]() определяют передаточный коэффициент
определяют передаточный коэффициент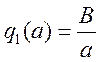 . В этом случае передаточная функция
нелинейного элемента определяется как комплексная величина:
. В этом случае передаточная функция
нелинейного элемента определяется как комплексная величина:
![]()
Рассмотрим разложение в ряд Фурье входного сигнала:
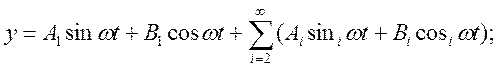
Аппроксимация выходного
сигнала первыми двумя членами ряда![]() называется
гармонической линеаризацией.
называется
гармонической линеаризацией.
Рассмотрим структурную схему управления с обратной связью:

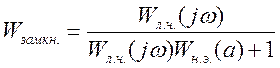
Уравнением гармонического
баланса называется такое соотношение для амплитуды и частоты автоколебаний ![]() и
и ![]() , для
которых справедливо равенство:
, для
которых справедливо равенство:
![]()
Для решения уравнения
гармонического баланса используют методы Гольдфарба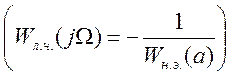 и
Коченбургера
и
Коченбургера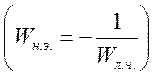 .
.
![]() функции
от параметров нелинейности
функции
от параметров нелинейности
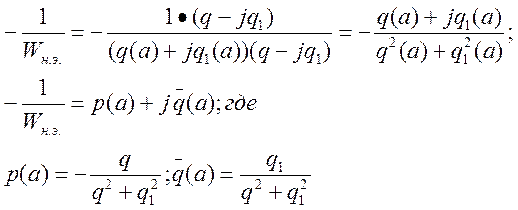
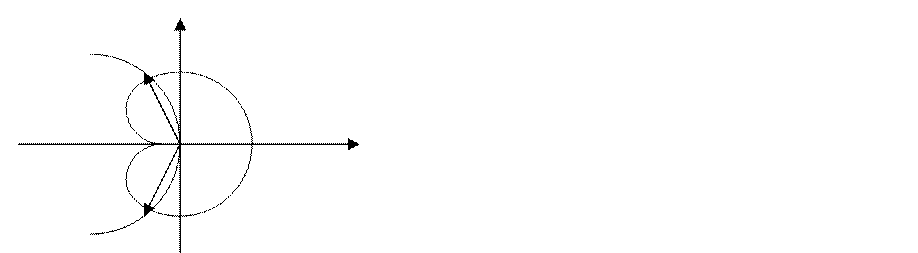
По методу Гольдфарба амплитуда и частота автоколебаний определяются в точке пересечения годографа линейной части системы с годографом нелинейной статической характеристики.
Точка, где годограф нелинейной части входит внутрь годографа линейной части с увеличением амплитуды, эта точка соответствует устойчивому режиму автоколебаний. А в точке выхода из области ограниченной линейной частью обычно режим автоколебаний неустойчивый.
Условие Гольдфарба является необходимым, но не достаточным; для неоднозначной нелинейной статической характеристики строгих доказательств нет.
Устойчивость нелинейной системы при исчезающе-малых воздействиях. Критерий устойчивости Попова.
Исследование нелинейной системы включает анализ следующих воздействий:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.