Передаточные функции экстраполятора определяют соотношения между входным сигналом и управляющим сигналом на выходе ЦАП при статическом законе управления.
1) Экстраполяция ступенчатым законом управления
![]()
2) Экстраполятор порядка 0
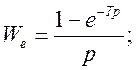
3) Экстраполятор порядка 1
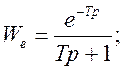
4) Экстраполятор порядка 2
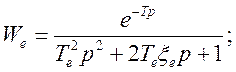
Для идеального вычислителя в форме статического звена передаточная функция разомкнутой системы с цифровой системой управления в обратной связи имеет следующий вид:
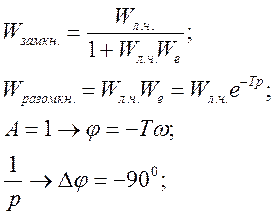
Выводы: Цифровая система управления при линейном статическом законе управления не изменяет амплитудную характеристику эквивалентной разомкнутой системы с отрицательной единичной обратной связью. Дискретность по времени цифровой системы управления приводит к увеличению фазового запаздывания. К фазовой характеристике разомкнутой системы линейной части необходимо добавить фазовое запаздывание , где -шаг дискретности. Это фазовое запаздывание связано с дискретностью по времени. В зависимости от выбора экстраполятора вносится фазовое запаздывание выбранным алгоритмом экстраполяции. Экстраполятор нулевого порядка изменяет непрерывно управляющий сигнал от предыдущего значения к последующему линейно по времени. Такой закон вносит запаздывание по фазе на-90. В случае использования экстраполяторов 1-го и 2-го порядка изменение фазовой характеристики составляет от 0 до -90 или -180. На частоте запаздывание по фазе составляет -45 для экстраполятора 1-го порядка и -90 для экстраполятора 2-го порядка.
![]() -для
экстраполятора 1-го порядка
-для
экстраполятора 1-го порядка
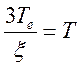 -для
экстраполятора 2-го порядка
-для
экстраполятора 2-го порядка
Динамика и передаточные функции вычислительного устройства.
Для описания работы динамической системы с дискретными управляющими устройствами используются несколько математических моделей для описания преобразования непрерывных и дискретных сигналов.
В качестве базовых вариантов рассматриваются преобразования системы ступенчатых сигналов, дискретные преобразования Лапласа и Z-преобразования.
Модель системы импульсных управляющих воздействий.
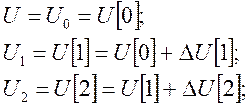

Модель системы ступенчатых воздействий позволяет рассматривать динамику линейной системы с цифровой системой управления в следующей форме.
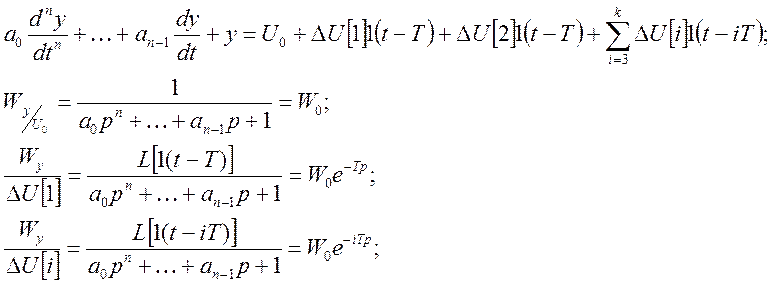
Передаточная функция линейной системы представляет собой передаточную функцию по отношению к сумме импульсных воздействий, смещенных по времени на интервал дискретности T.
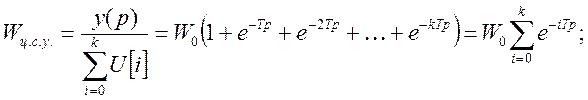
С учетом частного решения для уравнения экстраполятора в определении переходного процесса учитывается уравнение экстраполятора.
![]() -алгоритм
экстраполяции
-алгоритм
экстраполяции
Обозначим переходную функцию следующей величиной:
![]() переходная
функция на
переходная
функция на![]()

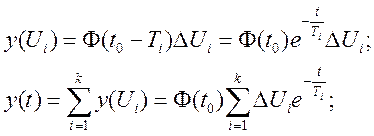
Передаточные функции дискретных систем управления и устойчивость технической системы с цифровыми управляющими устройствами.
Для описания дискретных функций и передаточных функций дискретных систем используются дискретные преобразования Лапласа и Z-преобразования.
В основе обоих методов лежит следующее представление дискретных функций.
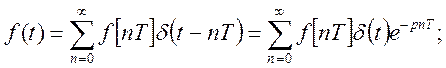
![]() -единичная
импульсная функция.
-единичная
импульсная функция.
Дискретные преобразования Лапласа.
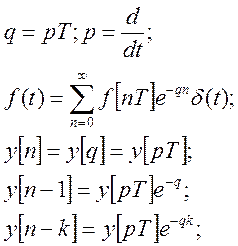
Эти соотношения используются для определения п.ф. по уровню в разностной форме.
Дано: разностное уравнение
![]()
После ДПЛ (дискретные преобразования Лапласа)
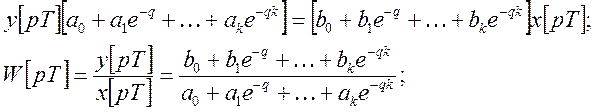
Для исследования устойчивости рассматривается характеристическое уравнение:
![]()
Корни должны иметь
отрицательную вещественную часть и по коэффициентам![]() составляют матрицу Гурвица и проверяется положительная определенность всех
диагональных миноров и матрицы Гурвица в целом.
составляют матрицу Гурвица и проверяется положительная определенность всех
диагональных миноров и матрицы Гурвица в целом.
Z-преобразования.
В качестве переменной Z
выбирается значение![]() или
или![]() .
.
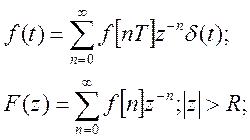
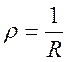 -радиус
сходимости
-радиус
сходимости
Z-преобразования обладает свойствами линейности, аддитивности и другими свойствами, характерными для линейных систем.
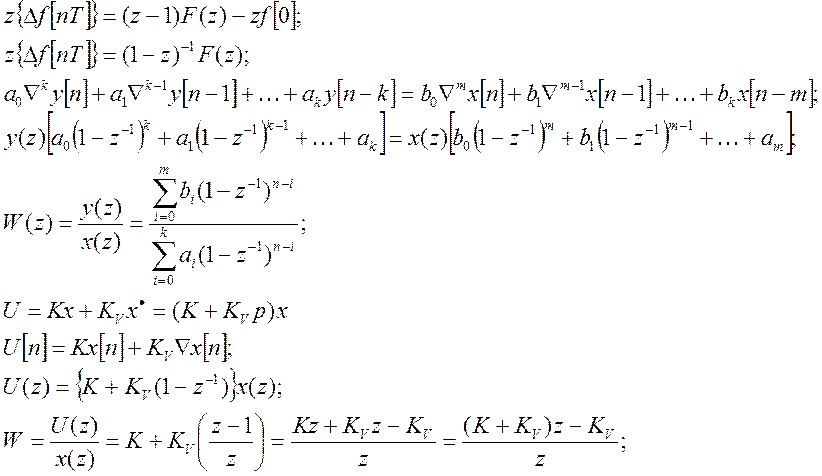
Линейный автопилот запаздывания.
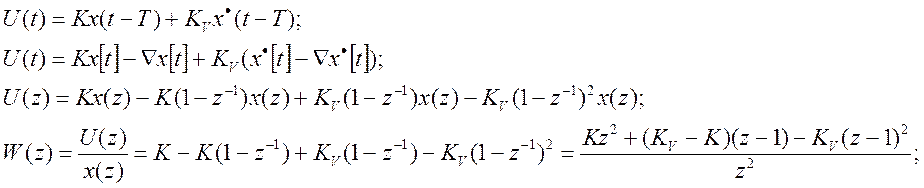
Для исследования устойчивости в частотной области используют аналоговые преобразования Фурье.
Замечание: рассмотрим гармоническое входное воздействие
![]()
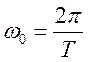 -частота
Котельникова для квантования системы с шагом дискретности по времени T.
-частота
Котельникова для квантования системы с шагом дискретности по времени T.
При большем значении частоты невозможно определить характеристики входного сигнала. При меньшем значении частоты решетчатая функция может быть использована для определения непрерывного входного сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.