Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления, страница 6

Если

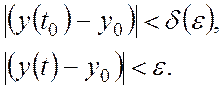
В случае, если , то есть при любом начальном отклонении выполняются неравенства Ляпунова, то динамическая система называется устойчивой в большом.

Если неравенства Ляпунова справедливы для ограниченного интервала времени, то есть при

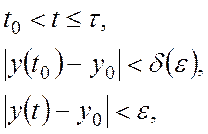
то система называется устойчивой на интервале.

Динамическая система будет устойчивой на неограниченном интервале, если неравенства Ляпунова выполняются при τ→∞.

Система будет устойчива в целом, если выполняются следующие неравенства:

при

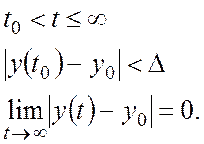
Устойчивость при начальных отклонениях от начала равновесия динамической системы. Теорема Ляпунова.

Классическое понимание устойчивости характеризует устойчивость динамической системы при начальных отклонениях от положения равновесия. Фазовое положение  – устойчивое фазовое состояние характеризуется такой функциональной зависимостью , что при

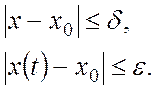
Если 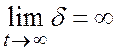 – устойчива в большом.

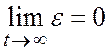 – асимптотически устойчива.

Теорема Ляпунова:

Линейная динамическая система устойчива, если для ее фазовых координат можно указать такую положительно–определенную функцию Ляпунова , что ее производная будет отрицательно определена. Если производная строго отрицательна, то система асимптотически устойчива.

Дано:

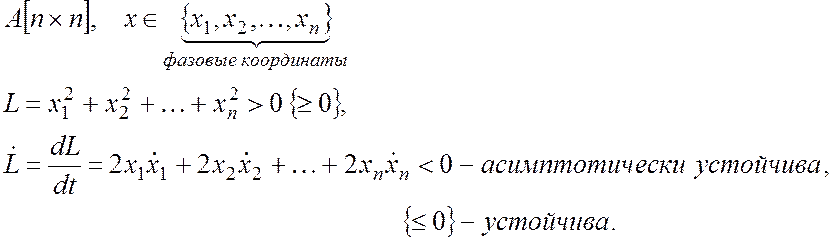
Доказательство:

Функция Ляпунова представляет собой квадрат расстояния от начала координат или, в общем случае, рассматривается как некоторая норма пространства размерности n.

В этом случае производная функции Ляпунова представляет собой направление вектора движения динамической системы в каждой точке фазового пространства. В случае отрицательного значения производной функции Ляпунова вектор движения направлен в сторону положения равновесия. Это необходимо и достаточно для устойчивого движения линейной динамической системы.

Пример:

Определить, устойчивы системы или неустойчивы.

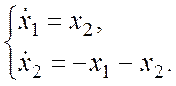
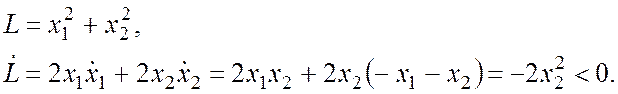
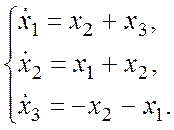
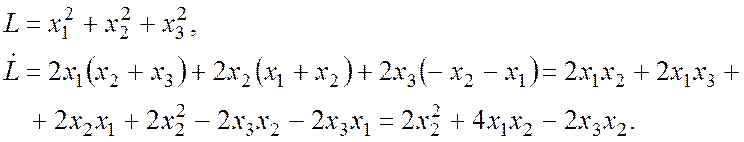
Система является неустойчивой, так как первое слагаемое строго больше нуля, а два других являются знакопеременными.

В общем случае, для линейных систем большого порядка выбор функции Ляпунова является достаточно сложным, и устойчивость исследуется другими методами.

Теорема Четаева.

Если для линейной динамической системы существует знако–определенная отрицательная функция, производная которой является положительно–определенной, то линейная динамическая система устойчива.

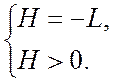
Теорема Михайлова.

Если для линейной динамической системы можно указать такую функцию, производная которой будет иметь противоположный знак, то линейная динамическая система будет устойчивой.

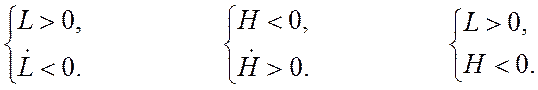
Устойчивость при исчезающе–малых воздействиях.

Рассматривается линейная динамическая система, находящаяся в равновесии.

В момент  на динамическую систему действуют исчезающее–малые воздействия , которые удовлетворяют следующим требованиям:

1. 

2. 

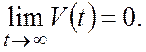
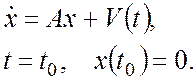
Определение устойчивости Попова.

1.  Линейная динамическая система называется устойчивой в малом, если можно указать такое максимальное значение , что при выполнении условия:

существует такое число , что выполняется условие:

2.  Если предел 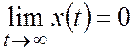, то динамическая система называется асимптотически устойчивой.

3.  Если система сохраняет устойчивость при стремлении  и при этом , то система устойчива в большом.

4.  Если при , , 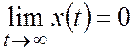то линейная динамическая система устойчива в целом.

Техническая интерпретация и практическое приложение.

Устойчивость при исчезающее–малых воздействиях интерпретируется как возврат технической системы в устойчивое положение после импульсных воздействий, аналогами которого является дача рулей самолета в установившемся полете.

Графическая интерпретация.

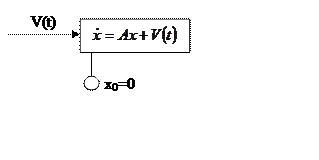
При построении импульсной переходной функции длительность импульса стремится к нулю, его величина стремится к бесконечности, а интеграл от импульсной функции по времени равен 1.

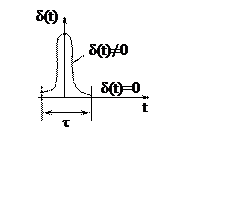
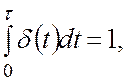
Устойчивость и управляемость автоматических систем.

Рассматривается динамика линейной системы, ранее находившейся в состоянии равновесия при постоянном управляющем воздействии.

–фазовые координаты,

–управляющий вектор.