Линейный анализ систем управления. Исследование элементов линейной системы управления. Пакет Control Toolbox и его использование для расчета систем управления, страница 19

1) гармоническое воздействие

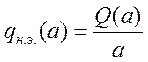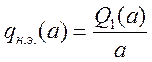-передаточная функция нелинейного элемента по форме колебаний

- передаточная функция нелинейного элемента по форме колебаний

Для нелинейной системы в отличии от линейной передаточные числа по формам колебаний изависят от амплитуды входного воздействия a.

Для нелинейной динамической системы анализ характеристик включает расчет зависимости амплитуды на выходе от частоты колебаний, а также от амплитуды входного сигнала.

2) Исследование автоколебаний нелинейной системы при начальных отклонениях от положения равновесия

При начальных отклонениях нелинейной системы возбуждает автоматические колебания выходной координаты в результате свободного движения в зоне нечувствительности нелинейного элемента и ограничение управления за пределами линейного регулирования.

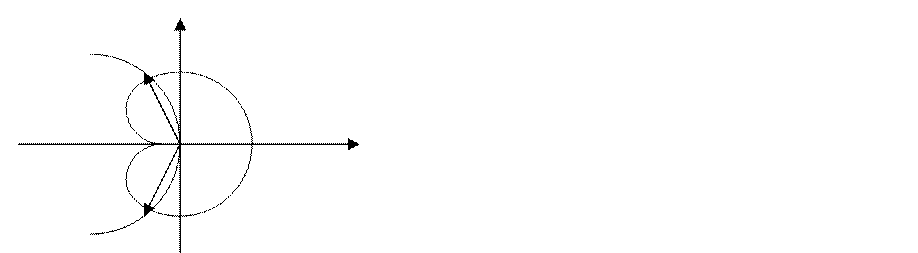
Необходимым условием существования автоколебаний является пересечение годографа передаточной функции линейной части системы годографом        , вычисленного для заданной нелинейности.

3) Реакция нелинейной системы на исчезающе-малые и импульсные воздействия.

Входной сигнал x(t) обладает следующими свойствами:

1)

2)

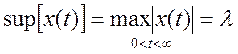
Входное воздействие x(t) рассматривается как исчезающе-малое, если его предел при времени стремящимся к бесконечности =0, а max значение из всех возможных значений ограничено по модулю и не превышает.

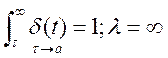
Устойчивость нелинейной системы при исчезающе-малых воздействиях.

Реакцию нелинейной системы на исчезающе-малые воздействия с использованием импульсной переходной функции.

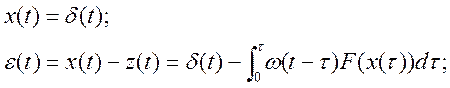
импульсная переходная функция линейной системы

Преобразования Лапласа:

Определение Ляпунова устойчивости нелинейной системы при исчезающее-малых воздействиях:

Нелинейная динамическая система при внешних исчезающее-малых воздействиях считается устойчивой, если при ограниченном по модулю входном воздействии можно указать такое малое число, что:

Т.о.положение равновесия y=0 называется устойчивым для нелинейной системы если при стремлении внешнего воздействия к 0 после достижения max значениявыходной координаты совершает колебания с амплитудой не болееотносительно положения равновесия.

Основные понятия и определения:

1) Если можно указать такую, что привыполняется условие устойчивости Ляпунова для нелинейных систем и приусловие Ляпунова не выполняется, то нелинейная система называется устойчивой в большом и малом при; а при   система устойчива в малом и неустойчива в большом.

2) Если и нелинейная система устойчива при любой, то нелинейная система называется устойчивой в целом.

Устойчивость нелинейной системы с характеристикой заданного класса.

Рассмотрим нелинейную систему с нелинейной характеристикой F(x), обладает свойствами определенного класса.

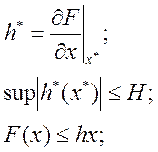
При выполнении данных соотношений нелинейный элемент представляет собой элемент класса H с ограничением коэффициента усиления.

Интерпретация класса нелинейного элемента:

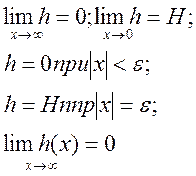
при

Последний нелинейный элемент (идеальное реле) относится к классу элементов с бесконечным коэффициентом усиления.

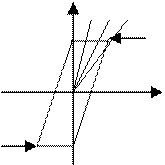
Т.о. в случае неоднозначной нелинейной характеристики с гистерезисом возможно изменение коэффициента усиления по знаку, т.е. отрицательная обратная связь при определенных условиях движения приобретает свойство положительной обратной связи.

Постановка задачи синтеза линейной части для обеспечения устойчивости замкнутой системы с нелинейной характеристикой заданного класса.

Рассмотрим линейную часть с передаточной функцией апериодического и колебательного звеньев.

Рассмотрим нелинейную систему с апериодической передаточной функцией линейной части является устойчивой в целом при любом коэффициенте усиления в цепи обратной связи.

Данное утверждение справедливо для класса нелинейных элементов с бесконечно большим коэффициентом усиления.

Рассмотрим линейную часть в виде колебательного звена: