Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 9

Знайдемо обернену матрицю (X^ТХ)^-1 (функція Excel МОБР(<діапазон>)). А потім обчислимо добуток матриць (X^ТХ)^-1(X^ТY).

	1,61904	-0,6785	0,05952			37,414	=а0
(XТХ)-1	-0,6785	0,34134	-0,0324		(XТХ)-1(XТY)	-2,228	=а1
	0,05952	-0,0324	0,00324			0,270	=а2

За значеннями обчислених параметрів записуємо рівняння регресії 37, 414-2,228x+0,270x².

Обчислимо коефіцієнт  лінійної кореляції r_xyза допомогою функції КОРРЕЛ(<діапазон>). r_xy= 0,59857 – слабкий лінійний зв'язок.

Знайдемо коефіцієнт детермінації

            R²= 1-.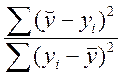

Для цього проведемо обчислення у вигляді таблиці

										Сума
x	1,00	2,00	3,00	4,00	5,00	6,00	7,00	8,00	9,00	45,00
y	35,40	34,20	33,60	32,10	32,70	33,80	35,60	37,20	38,80	313,40	Ysr= 34,82
	35,46	34,04	33,16	32,82	33,02	33,76	35,05	36,87	39,23	313,40
	0,40	0,62	2,77	4,01	3,24	1,12	0,05	4,18	19,42	35,80
	0,33	0,39	1,49	7,41	4,50	1,04	0,60	5,65	15,82	37,26
	0,00	0,03	0,19	0,52	0,10	0,00	0,31	0,11	0,18	1,45

R²=0,9611, отже, наша модель добре описує вхідні дані.

Оцінимо адекватність моделі за критерієм Фішера. Обчислюємо

F_р=,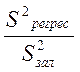

де S²_регрес =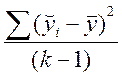 =17,90, S²_зал =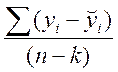 =0, 24,

F_р=74,0492.

Знаходимо F_кр=F(a, k-1,n-k) , k-кількість параметрів. F_кр визначаємо за допомогою функції  FРАСПОБР(0,01;2;6), F_кр=10,9249. Оскільки F_р >F_кр  модель адекватна.

Побудуємо графік:

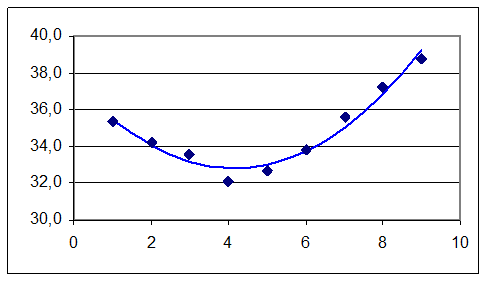
Тепер ми можемо зробити прогноз витрат на рекламу до кінця  року. Для цього ми використовуємо наше рівняння регресії 37, 414-2,229x+0,270x². Будуємо таблицю вхідних значень y та значень , обчислених за отриманим рівнянням регресії (y_регр) .

x	y	yрегр
1	35,4	35,45
2	34,2	34,03
3	33,6	33,159
4	32,1	32,82
5	32,7	33,022
6	33,8	33,764
7	35,6	35,045
8	37,2	36,86
9	38,8	39,229
10		42,13
11		45,573
12		49,55

Будуємо графік:

 

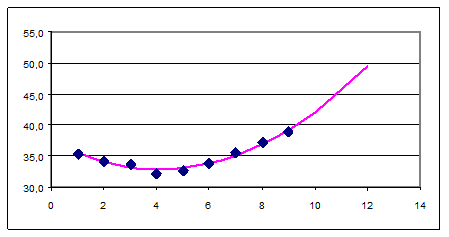
Висновок: на кінець року витрати на рекламу складуть 49,55 тис. грн.

7.11 Множинний регресійний аналіз

До цього часу ми розглядали регресійний зв'язок між двома ознаками. Якщо на досліджувану змінну впливає декілька факторів, то регресію називають множинною.

Нехай для визначення впливу факторів X₁, X₂, …,X_m на значення величини Y  проведено n вимірювань. Отримані значення можна подати у вигляді таблиці.

X1	X2	Xm	Y
X11	X12	X1m	Y1
X21	X22	X2m	Y2
...	...	...	...
Xn1	Xn2	Xnm	Yn

Будемо виходити з того, що між пояснюваною (залежною) змінною (Y) та факторами, що на неї впливають (X₁, X₂, …,X_m) обрано лінійний зв'язок