Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 4

– називають непоясненими відхиленнями, тобто відхиленнями, які не можна пояснити за допомогою регресійної прямої.

Зведемо (7.8) у квадрат і обчислимо суму за всіма значеннями і:

;

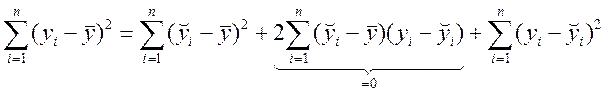Розділимо на n:

;

.

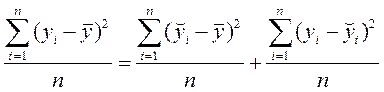Оскільки модель відображає вплив на результативну ознаку лише частину реальних факторів, регресійний аналіз пояснює тільки частину дисперсії відгуку (загальної дисперсії).

Загальна дисперсія = дисперсія, що пояснюється регресійним аналізом + залишкова дисперсія.

,

,

де s²_заг – загальна дисперсія;

            s²_регр – дисперсія, що пояснюється регресією;

            s²_зал – дисперсія помилок.

7.5 Оцінка якості моделі

Для оцінки якості моделі вводиться коефіцієнт детермінації, що показує, яка частина варіації пояснюється за допомогою регресійної залежності

,

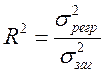або

.

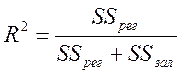Оскільки

,

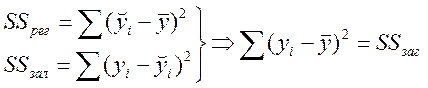тобто

,

то, остаточно,

.

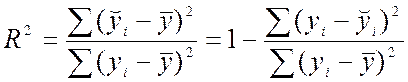Коефіцієнт детермінації показує, яка частина варіації результативної ознаки Y враховується в моделі й обумовлена впливом на неї незалежних факторів, врахованих у моделі. Можливі значення коефіцієнта детермінації належать відрізку [0;1]. Чим ближче R² до 1, тим краща якість моделі. Якість моделі вважається прийнятною, якщо коефіцієнт детермінації не нижче 0,96.

h – індекс кореляції. Він, як і R², відображає точність моделі й може використовуватися при будь-якій формі зв'язку. При прямолінійному зв'язку індекс кореляції дорівнює коефіцієнту кореляції.

,       .

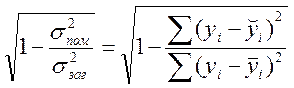Чим ближче  h до 1, тим краще регресійна залежність  описує експериментальні дані.

7.6 Критерій Фішера для оцінки адекватності  моделі

Побудуємо випадкову величину   

,

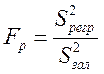де ,   k – кількість параметрів моделі. Для парної лінійної регресії k=2, ( k-1)=1;

 ,  n –кількість спостережень.

Обчислюємо  F _кр, для заданого рівня значущості α, використовуючи функцію FРАСПОБР  пакету Excel:  

F _кр = FРАСПОБР(a; k-1; n-k).

Якщо, то модель адекватна.

7.7 Перевірка значущості коефіцієнтів регресії

Для перевірки значущості коефіцієнтів регресії застосовуємо  t – критерій Стьюдента, за допомогою якого перевіряють, чи значуще a_i відрізняється від нуля. Висуваємо гіпотези:

Н₀: ;      Н₁: ;

Обчислюємо критеріальне значення 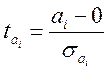, яке має розподіл Стьюдента з n-k ступенями вільності,

де; ;  ;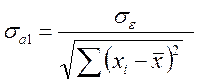

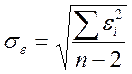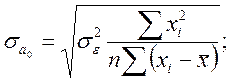
n – кількість спостережень; k – кількість параметрів регресії.

Обчислюємо для заданого рівня значущості α критичне значення .

Якщо , a_i – статистично незначуще, а якщо , a_i  - статистично значуще.

Якщо виникає ситуація, що a_i  статистично незначуще відрізняється від нуля, то це означає, що вплив i-го фактору на досліджувану змінну нестабільний.

7.8 Функції Excel для побудови регресійних залежностей

В Excel для знаходження кращої залежності необхідно побудувати лінію тренда.

1  Будується графік.

2  На графіку виводимо контекстне меню – Додати  лінію тренда.

3  Обираємо тип лінії тренда (лінійна, логарифмічна, експонентна, степенева).

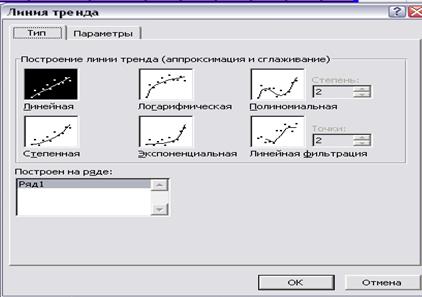
4  У закладці Параметры обираємо:

-  показывать уравнение на диаграмме;

-  поместить на диаграмму величину достоверности аппроксимации (R^2).

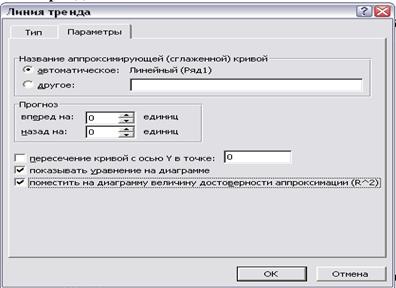
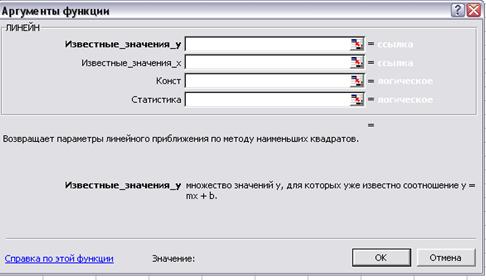
В Excel для побудови лінійної регресії використовується функція линейн, що дає рівняння лінійної регресії (=a₁х+a₀) і статистику. Цю функцію можна також використовувати для множинної  регресії = a_mх_m+…+ a₂х₂+ a₁х+a₀ (m змінних впливають на досліджуваний фактор).

• необхідно виділити 5 рядків і k стовпців, де k - кількість параметрів моделі;
• вибрати функцію Линейн;

• зазначити параметри: діапазон значень Y; діапазон значень X;
• зазначити вигляд регресії:  

= a_mх_m+…+ a₂х₂+ a₁х+a₀ в графі Конст ставимо 1 (истина),

якщо = a_mх_m+…+ a₂х₂+ a₁х в графі Конст ставимо 0 (ложь).

·  Статистика — логічне значення, що вказує, чи потрібно повернути додаткову статистику для регресії.  Якщо аргумент статистика має значення ИСТИНА, то функція ЛИНЕЙН повертає додаткову регресійну статистику.

Натиснути CTRL+Shift+Enter для введення значень масиву.

Отримаємо таблицю результатів: