Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 18

Q – загальна сума квадратів відхилень спостережуваних значень  від загального середнього .

Знаючи Q, Q₁ , Q₂, можна оцінити відповідні дисперсії, тобто загальну, міжгрупову (факторну) і внутрішньогрупову (залишкову):

;     ;   ;

.

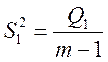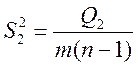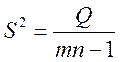Звичайно розраховують Q і Q₁, а потім обчислюють

Q₂ = Q-Q₁.

Для того, щоб перевірити при заданому рівні значущості α гіпотезу про рівність середніх декількох (m>2) нормальних сукупностей з невідомими, але однаковими дисперсіями, досить перевірити за критерієм Фішера гіпотезу про рівність факторної й залишкової дисперсії S₁=S₂ .

Якщо вплив всіх рівнів фактора g однаковий,  то S₁ і S₂ – оцінки загальної дисперсії, тому відрізняються незначуще.

 Гіпотези:

Н₀ : S₁² = S₂²;             H₁ : S₁² > S₂².

Розраховуємо  F_р = 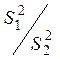 , що має розподіл Фішера з k₁= m-1 і k₂ = m(n-1) ступенями вільності.

При заданому рівні значення aобчислюють критичне значення F_кр =F(a; k₁; k₂).

Якщо F_р > F_кр, то  Н₀  відкидається й робиться висновок про істотний вплив фактора γ.

Якщо F_p  < F_кр – немає підстави відкидати гіпотезу Н₀ і вважають, що вплив фактора γ несуттєвий.

Для більш повного розуміння, як будується F-статистика для перевірки гіпотези H₀ , запишемо

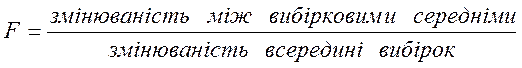
Порівнюючи міжгрупову та залишкову дисперсії, за величиною їх відношення судять, наскільки сильно проявляється вплив фактора.

Однофакторний аналіз зручно подавати у вигляді таблиці.

Компоненти дисперсії	Сума квадратів, (SS)	Число ступенів  вільності, (DS)	Дисперсія (MS)
Міжгрупова		m-1
Внутрішньо- групова		m(n-1)
Загальна		mn-1

 

Приклад. Необхідно виявити, чи впливає відстань від центра міста на ступінь заповнюваності готелів. Нехай введені 3 рівні відстаней від центра міста: 1) до 3 км, 2) від 3 до 5 км і 3) понад 5 км. Дані заповнюваності представлені в таблиці.

Відстань	Заповнюваність
До 3 км	92 98 89 97 90 94
Від 3 до 5 км	90 86 84 91 83 82
Понад 5 км	87 79 74 85 73 77

Розв’язання.

Число вибірок m=3, число досліджених готелів для кожної вибірки  n=6, загальна кількість спостережень  mn=18.

Обчислимо середні значення для кожної вибірки  і загальне середнє :

 =93,333     = 86    =79,167   =86, 167.

Після чого знайдемо значення Q, Q₁, Q₂:

=904,5, 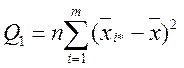 =602,33,

Q₂ = Q – Q₁=302,167.

Обчислюємо міжгрупову дисперсію S₁ та залишкову S₂:

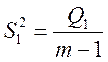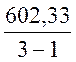=   =301,167,

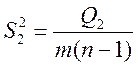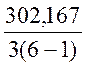==20,444.

Висуваємо гіпотези:

Н₀ : S₁² = S₂²;             H₁ : S₁² > S₂².

Розраховуємо  F_р = 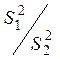=14,95, та при заданому рівні значення a=0,05  обчислюємо критичне значення F_кр =FРАСПОБР(0,05; 3-1; 3×(6-1))= 3,682.

Оскільки F_р > F_кр, то гіпотезу Н₀  відкидаємо і робимо висновок про істотний вплив фактора, тобто фактор відстані від центра міста значуще впливає на ефективність заповнення готелів.

В Excel  для проведення дисперсійного аналізу можна скористатися  Сервис –Анализ данных – Однофакторный дисперсионныйанализ.

1  Досліджувані дані введіть у робочу таблицю Excel (діапазон А1:F3).

2  Виберіть пункт меню Сервис – Анализ данных. У діалоговому вікні Анализ данных у списку Инструменты анализа виберіть процедуру Однофакторный дисперсионныйанализ. Натисніть кнопку ОК. На екрані з’явиться вікно

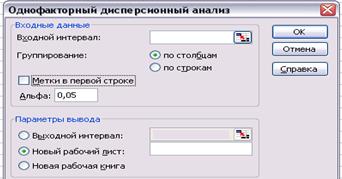
3  В  діалоговому вікні Однофакторный дисперсионный анализ у полі Входной интервал задайте А1:F3.

4  У розділі Группирование перемикач встановіть в положення по строкам.

5  Зазначте Выходной интервал і натисніть Ок.

У результаті буде отримана така таблиця: