Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 7

Неважко помітити, що матриця є матрицею системи нормальних рівнянь, з якої визначається вектор , компонентами якого є Мнк-оцінки  параметрів а₀, а₁, ..., а_m моделі (7.9). Вектор-стовпець правих частин системи можна подати у вигляді , тому матричний запис цієї системи наступний:

.                                  (7.13)

Помножимо ліву й праву частини (7.13) ліворуч на обернену матрицю . Оскільки  – одинична матриця порядку m+1, за властивостями одиничної матриці з (7.13) маємо 

.

7.10 Метод найменших квадратів при оцінюванні параметрів поліномів

Якщо аналіз діаграми розсіювання дозволить висунути гіпотезу про поліноміальний зв'язок між змінними Y і X:

,                     (7.14)

то в цьому випадку функція помилок є квадратичною функцією параметрів a₀,...,a_m,  a часткові похідні  – лінійні щодо параметрів.

Для того щоб знайти a₀, ..., a_{m ,} використовується МНК.

Умова 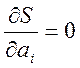 ( ) дозволяє одержати систему рівнянь:

.

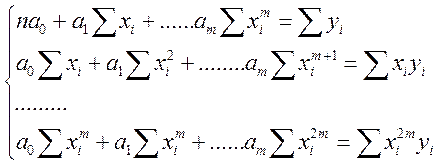Система містить m+1 рівняння з m+1 невідомим. Якщо m< n-1, то система має єдиний розв’язок.

Запишемо систему рівнянь у матричному вигляді. Розглянемо вектори-стовпці

,                                       

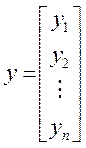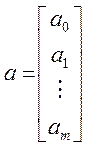
і матрицю розмірності n (m+1):

,                

.                                                     

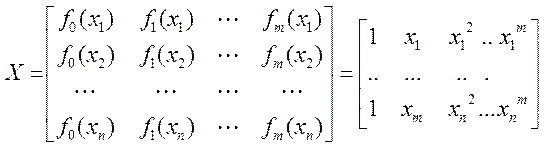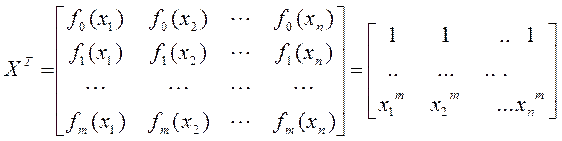Вектор-стовпець правих частин системи рівнянь можна представити у вигляді , тому матричний запис цієї системи такий:

.

Помножимо ліву й праву частини ліворуч на обернену матрицю . Одержимо

            .                                 (7.15)

У випадку параболічної регресії   система має вигляд

.

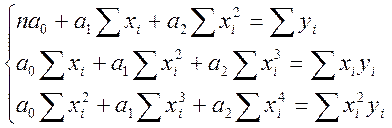У статистиці використовують правило вибору ступеня полінома (7.14), яке базується на визначенні величини кінцевих різниць (якщо x змінюється з постійним кроком) або розділених різниць (якщо крок  const).

Кінцева різниця 1-го порядку

   ,           .

Розділена різниця    

            ,

,     .

Якщо перші різниці постійні, то для моделі обирається поліном першого  ступеня.

Якщо перші різниці не постійні, але варіюються з незначними відхиленнями, і середнє арифметичне двох різниць настільки мале, що ним можна знехтувати, то перші різниці вважаються практично рівними.

Аналогічно, якщо аналізуються другі різниці, і ми прийдемо до висновку, що вони практично рівні, то для відображення ряду емпіричних даних використовують поліном другого ступеня й т.д.

Коефіцієнт детермінації R² розраховується так,  як і для лінійної регресії:

 .

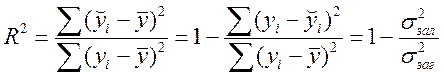Адекватність моделі. Розраховуємо критеріальне значення 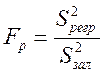 та критичне значення , де ; ; α – рівень значущості; k – кількість параметрів моделі, n – кількість спостережень.

Значення F_кр   обчислюємо за допомогою функції  FРАСПОБР(α; k-1; n-k).  Якщо F_p>F_kp  –  модель адекватна.

Приклад. Нехай для деякого підприємства відомі середні витрати на рекламу (Y тис. грн) за останні n місяців (Х).

X	1	2	3	4	5	6	7	8	9
Y	35,4	34,2	33,6	32,1	32,7	33,8	35,6	37,2	38,8

Необхідно:

ü  записати систему рівнянь для визначення невідомих параметрів рівняння поліноміальної регресії другого порядку =a₀+a₁x+a₂x² ;

ü  знайти параметри регресії;

ü  обчислити коефіцієнт  лінійної кореляції;

ü  знайти коефіцієнт детермінації;

ü  оцінити адекватність моделі за критерієм Фішера при рівні значущості α=0,01;

ü  побудувати графік;

ü  зробити прогноз витрат на рекламу до кінця року.

Розв’язання

Рівняння регресії має вигляд =a₀+a₁x+a₂x². Для визначення невідомих параметрів регресії (а₀, а₁ , а₂) необхідно записати систему рівнянь.

Коефіцієнти даної регресії обчислимо за допомогою методу найменших квадратів. Система буде мати такий вигляд

                .

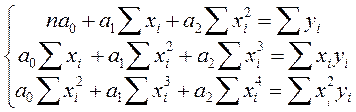Обчисливши зазначені суми, одержимо систему рівнянь