Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 11

При правильному включенні факторів у регресійну модель величина індексу множинної кореляції буде істотно відрізнятися від індексу кореляції парної залежності. Якщо ж додатково включені в рівняння множинної регресії фактори третьорядні, то індекс множинної кореляції може практично збігатися з індексом парної кореляції (розбіжності в третьому, четвертому знаках). Звідси зрозуміло, що, порівнюючи індекси множинної й парної кореляції, можна зробити висновок про доцільність включення в рівняння регресії того чи іншого фактора.

Приклад.  Нехай є наступні дані (умовні) про змінний видобуток вугілля на одного робітника y, (т); потужності шару x₁, (м); і рівні механізації робіт x₂,(%); що характеризують процес видобутку вугілля в 10 шахтах.

№ шахти	1	2	3	4	5	6	7	8	9	10
X1	8	11	12	9	8	8	9	9	8	12
X2	5	8	8	5	7	8	6	4	4	7
Y	5	11	10	6	6	7	6	5	5	11

Необхідно:

1  обчислити парні і часткові коефіцієнти кореляції, провести їх аналіз;

2  знайти параметри лінійної множинної регресії   =a₀+a₁x₁+a₂x₂ матричним способом;

3  знайти параметри лінійної множинної регресії  =a₀+a₁x₁+a₂x₂ за допомогою функції ЛИНЕЙН;

4  перевірити значущість параметрів регресії;

5  знайти коефіцієнт детермінації, оцінити якість моделі;

6  оцінити адекватність моделі за критерієм Фішера при рівні значущості α=0,05.

Розв’язання.

1 Обчислимо парні коефіцієнти кореляції.

Використовуємо Сервис – Анализ данных – Корреляция.

Одержимо кореляційну матрицю

		X1	X2	Y
		Строка 1	Строка 2	Строка 3
X1	Строка 1	1
X2	Строка 2	0,508	1
Y	Строка 3	0,901	0,7619	1

Отже відповідні коефіцієнти парної кореляції такі:

r_Y1=0,901;  r_Y2= 0,7619;  r₁₂=0,508.

Обчислимо коефіцієнти часткової кореляції за формулами

 ,    ,

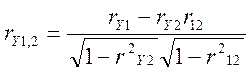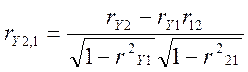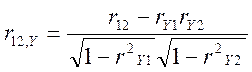
Отримаємо такі данні:

ry1,2	=	0,921637
ry2,1	=	0,814348
r12,y	=	-0,63603

Проведемо аналіз отриманих коефіцієнтів парної та часткової кореляції.

 Додатне значення r_y1 свідчить про прямий зв'язок між Y та X₁, r_y1=0,901, отже вплив потужності шару X₁ на видобуток вугілля сильний. Усунення X₂ збільшує кореляційний зв'язок (r_y1,2 = 0,921637).

Додатне значення r_y2 свідчить про прямий зв'язок між Y та X₂, оскільки r_y2=0,7619 – зв'язок обсягу видобутку вугілля й рівня механізації робіт X₂ суттєвий.  Усунення Х₁ цей зв'язок підсилює (r_y2,1 = 0,814348).

r₁₂=0,508 свідчить про те, що X₁ і X₂ практично не корелюють. Це важливо в регресійних моделях. Однак усунення Y не послабляє кореляцію (r_12,y = -0,63603).

2 Оцінимо невідомі параметри множинної лінійної регресії.

Рівняння регресії має вигляд =a₀+a₁x₁+a₂x₂. Для визначення невідомих параметрів регресії (а₀, а₁ , а₂) необхідно записати систему рівнянь у матричній формі.

.

Запишемо матриці X таY .

X			Y
1	8	5	5
1	11	8	11
1	12	8	10
1	9	5	6
1	8	7	6
1	8	8	7
1	9	6	6
1	9	4	5
1	8	5	5
1	12	7	11

Обчислимо X^Т за допомогою функції Excel ТРАНСП( <масив>).