Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 2

,

тоді рівняння

                           

буде лінійним рівнянням моделі.

Як перетворення часто використовують логарифмування,  знаходження оберненого значення.

Приклад. Вигляд функції регресії . Тоді випадкову величину Y можна представити у вигляді:  –  нелінійна модель. Прологарифмуємо це рівняння й одержимо

.

Позначимо y^*=lny, a₀^*=lna₀, x^*=lnx, тоді  буде лінійним рівнянням моделі.

IV припущення:  про властивості розподілу ймовірностей для випадкового збурювання

            1)  , .

            2)  У кожному досліді  дисперсія постійна й не залежить від X

,           ,

- невідома, але постійна величина.

3)  Помилки в будь-яких двох дослідах незалежні

              .

Діаграма розсіювання дозволяє зробити візуальний аналіз емпіричних даних. Однак існують і більш точні, теоретично обґрунтовані методи виявлення закономірного зв'язку між випадковими змінними Y і X. Найпоширенішим з них є метод Фостера - Стюарта. Він дозволяє не тільки встановити наявність тенденції у зв'язку кількісних ознак Y і X, але й перевірити гіпотезу  про сталість дисперсії випадкового збурювання. Суть методу полягає в наступному.

1  Порівнюється кожен рівень ряду з усіма попередніми, при цьому

        f_i  = 1,   e_i  = 0,   якщо Y_i  > Y_k ,   k=1, 2,..., i-1;

     f_i = 0,   e_i  = 1,   якщо Y_i < Y_k ,   k=1, 2,..., i-1;

     f_i = 0,   e_i = 0   в інших випадках.

2  Обчислюються значення величин

   .

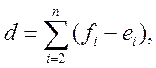
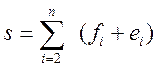Показники d і s характеризують тенденції у зв'язках Y і X і дисперсії  і  Х відповідно.

3 За допомогою t-критерію Стьюдента  перевіряється гіпотеза про те, чи можна вважати випадкові різниці d=0 і . Для цього знаходять величини

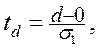
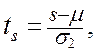                                         (7.2)

де - середнє значення величини s;  і  - стандартні помилки величин d і s відповідно. Значення величин , і  протабульовані й наведені в табл. 7.1.

4 При заданому рівні значущості порівнюються розраховані значення t_d  і  t_s  з табличним. Якщо t_d <  t_табл  і  t_s < t_табл, то гіпотеза про відсутність тенденцій у зв'язку Y і X та   і Х  підтверджується.

Таблиця 7.1 – Значення середньої  та стандартних похибок і  для n від 10 до 55

n
10	3,858	1,964	1,288
15	4,636	2,153	1,521
20	5,195	2,279	1,677
25	5,632	2,373	1,791
30	5,990	2,447	1,882
35	6,294	2,509	1,956
40	6,557	2,561	2,019
45	6,790	2,606	2,072
50	6,998	2,645	2,121
55	7,187	2,681	2,163

Як приклад, розглянемо визначення наявності тенденцій у ряді динаміки експорту товарів та послуг в Україні за 1993 – 2007 р.р. (табл. 7.2).

Таблиця 7.2 - Експорт товарів та послуг в Україні. Визначення f_i і e_i

№ п/п	Показники	Експорт товарів та послуг, млн. доларів США	fi	ei	di	si
1	1993	7817	0	0	0	0
2	1994	16641	1	0	1	1
3	1995	17090	1	0	1	1
4	1996	20346	1	0	1	1
5	1997	20355	1	0	1	1
6	1998	17621	0	0	0	0
7	1999	16332	0	0	0	0
8	2000	19248	0	0	0	0
9	2001	21086	1	0	1	1
10	2002	23351	1	0	1	1
Продовження табл. 7.2
11	2003	28953	1	0	1	1
12	2004	41291	1	0	1	1
13	2005	44378	1	0	1	1
14	2006	50239	1	0	1	1
15	2007	64001	1	0	1	1