Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 12

XТ
1	1	1	1	1	1	1	1	1	1
8	11	12	9	8	8	9	9	8	12
5	8	8	5	7	8	6	4	4	7

Обчислимо добутки матриць X^ТХ та X^ТY (функція Excel МУМНОЖ(<матриця 1>;< матриця 2>).

XТ				XТY
10	94	62		72
94	908	595		710
62	595	408		474

Знайдемо обернену матрицю (X^ТХ)^-1 (функція Excel МОБР(<діапазон>)). А потім обчислимо добуток матриць (X^ТХ)^-1(X^ТY).

(XТ)-1			(XТХ)-1(XТY)
3,849883	-0,34239	-0,08571	а0 =	-6,53302
-0,34239	0,055269	-0,02857	а1 =	1,04637
-0,08571	-0,02857	0,057143	а2 =	0,628571

За значеннями обчислених параметрів записуємо рівняння регресії y= -6,533+ 1,046x₁+ 0,6286x₂.

3 Використовуючи функцію ЛИНЕЙН, перевіряємо обчислення. Отримуємо такі дані:

0,6286	1,046	-6,533
0,1693	0,166	1,3897
0,9368	0,708
51,910	7
52,088	3,5119

Як бачимо з таблиці a₀ = -6,533, a₁ = 1,046, a₂ = 0,6286, R²= 0,9368, F_p= 51,910.

Одержуємо рівняння регресії  y= -6,533+ 1,046x₁+ 0,6286x₂.

Воно показує, що при збільшенні тільки потужності шару x₁ (при незмінномуx₂) на 1 м видобуток вугілля на одного робітника y збільшиться в середньому на 1,046 т, а при збільшенні тільки рівня механізації робіт x₂ (при незмінномуx₁) на 1% – у середньому на 0,6286 т.

4  Установимо значущість коефіцієнтів лінійної регресії. Обчислимо критеріальні значення t_ai = a_i /σ_ai.

                 

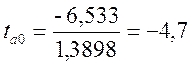
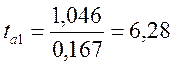
Задамо рівень значущості  та обчислимо критичне значення , де k – кількість параметрів регресії; n – кількість вимірювань.

t_kp=СТЬЮДРАСПОБР(0,05;7)=2,365

Якщо |t_ai | < t_kr – коефіцієнти статистично не значущі, у випадку |t_ai |> t_kr  –  коефіцієнти статистично значущі.

Висновок: коефіцієнти регресії а₀ , а₁, а₂ статистично значущі.

5 Перевіримо якість моделі. Коефіцієнт детермінації R²=0,936, скоригований коефіцієнт детермінації –=0,9188, що свідчить про прийнятну якість моделі.

6 Перевіримо адекватність моделі за критерієм Фішера. 

F_p=51,91, F_kp=FРАСПОБР(0,05; 2; 7)=19,35.

Як бачимо F_p > F_kp, отже модель адекватна.

Висновок: модель Y= -6,533+ 1,046x₁+ 0,6286x₂  +U якісна і адекватна.

7.12 Методи побудови багатофакторної регресійної моделі

7.12.1 Вибір "найкращого" рівняння регресії

Нехай відібрана множина факторів х₁,х₂,...,х_р, які впливають на досліджуваний показник Y. Є два протилежних критерії для вибору кінцевої моделі регресійного аналізу.

1 Якщо ми хочемо зробити модель корисною для прогнозу, то ми повинні включити якнайбільше факторів для того, щоб значення прогнозованої  величини було надійним.

2  Оскільки одержання інформації з послідовним контролем при збільшенні  кількості змінних  має потребу в більших витратах, варто прагнути, щоб модель включала по можливості менше факторів.

Компромісом між цими крайностями є те, що називають вибором "найкращого" рівняння регресії. Для реалізації такого вибору немає єдиної статистичної процедури. Взагалі ж існує досить велика кількість методів побудови регресійної моделі, найбільш відомими є:

1)  метод всіх можливих регресій;

2)  метод виключень;

3)  кроковий регресійний аналіз;

4)  деякі модифікації попередніх методів та ін.

Ми розглянемо лише найпоширеніші на практиці методи побудови лінійних регресійних моделей.

7.12.2 Метод усіх можливих регресій