Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 20

Ранговий аналіз використовують в тих випадках, коли величини, між якими досліджується наявність зв'язку, представлені не в шкалах відношень, а в будь-яких інших. Найчастіше така ситуація виникає, якщо ми маємо справу із суб'єктивними оцінками об'єктивних явищ, які не можна виміряти, тобто з експертними оцінками. Наприклад: досліджувати співвідношення між математичними й музичними здібностями учнів. Оцінки виставляються в балах.

Рангова кореляція використовується тоді, коли закон розподілу хоча б однієї з величин не є нормальним.

Коефіцієнт кореляції називають ранговим тому, що перед його обчисленням значення змінних перетворюють у ранги. Для цього значення змінних розміщують в упорядкованому ряді, потім кожному значенню присвоюють ранг від 1 до N, де N – кількість досліджуваних об'єктів.

Якщо кілька елементів мають однакові значення, то кожному з них присвоюється середнє значення від займаних ними місць.

Припущення:

• спостереження взаємно незалежні;
• N>9.

Тісноту зв'язку між рангами вимірюють так само, як і між ознаками. Розглянемо формулу коефіцієнта кореляції

,

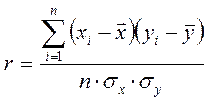
де ,       .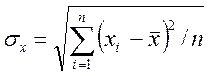

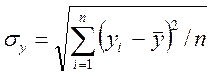Нехай              

,    ,

одержимо:

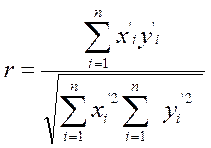                        (9.1)

Залежно від того,  що прийняти за міру розбіжності між величинами x′ і y′, можна одержати різні коефіцієнти зв'язку між рангами. Звичайно використовують коефіцієнти рангової кореляції Кенделла (τ) і Спірмена (ρ).

9.1 Коефіцієнт рангової кореляції Кенделла (Кендалла)

Введемо міру розбіжності між об'єктами (x_i ; x_j)

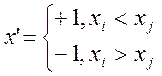
та відповідно для (y_i ; y_j)

.

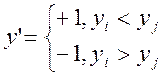Пояснимо це на прикладі.  Припустимо ми маємо дві послідовності. Необхідно з’ясувати, чи існує між ними зв'язок.

X	2	4	5	1	3
Y	1	5	3	4	2

Для полегшення обчислень одну із послідовностей (в нашому випадку це послідовність X), впорядковують таким чином, щоб її елементи були числами натурального ряду (розташовують за заростанням).  Змінюють і другу послідовність Y таким чином, щоб збереглась відповідність значень (x_i ;y_i).

Отримаємо таку таблицю

x	1	2	3	4	5
y	4	1	2	5	3

Розглянемо послідовність X. Першій парі (1; 2) припишемо значення 1, оскільки x₁<x₂, другій парі (1; 3) також припишемо значення 1, і т.д. Послідовно перебираємо всі пари, причому кожна пара повинна бути врахована один раз. Аналогічні обчислення проведемо для послідовності Y, причому  порядок перебору пар повинен в точності повторювати порядок перебору пар в послідовності Х. Результати обчислень наведені в таблиці 9.1.

Таблиця 9.1 

x	x′	y	y′	x′×y′
(1,2)	1	(4,1)	-1	-1
(1,3)	1	(4,2)	-1	-1
(1,4)	1	(4,5)	1	1
(1,5)	1	(4,3)	-1	-1
(2,3)	1	(1,2)	1	1
(2,4)	1	(1,5)	1	1
(2,5)	1	(1,3)	1	1
(3,4)	1	(2,5)	1	1
(3,5)	1	(2,3)	1	1
(4,5)	1	(5,3)	-1	-1
				=2

Розглянемо формулу (9.1). В нашому випадку 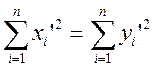 і дорівнює кількості пар, що беруть участь у переборі. Кожна пара зустрічається тільки один раз, тому їх кількість дорівнює числу сполучень з n по 2, тобто

.

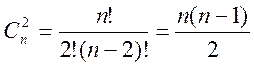Позначимо 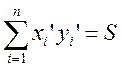, отримаємо формулу для обчислень   коефіцієнта рангової кореляції Кенделла

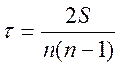 .                                     (9.2)

Коефіцієнт  Кенделла приймає значення з інтервалу    [-1;1].

Для нашого прикладу коефіцієнт рангової кореляції Кенделла дорівнює

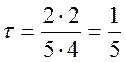=0,2.

9.2 Коефіцієнт рангової кореляції Спірмена

Коефіцієнт рангової кореляції Спірмена обчислюється за формулою

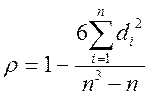 ,                                (9.3)