Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 6

Результати обчислень функції ЛИНЕЙН наведені на рис. 7.1.

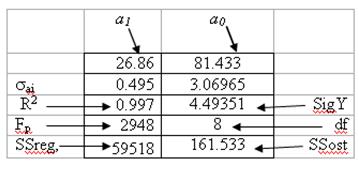
Рисунок 7.1 – Результати обчислень функції ЛИНЕЙН.

Як бачимо  а₀ =81,433, а₁=26,86. Отже, отримане рівняння     =26,86x + 81,433.

5    Обчислений коефіцієнт детермінації  R² =0,997.  Висновок: модель якісно описує вхідні дані.

6  Для оцінки адекватності  моделі використовуємо критерій Фішера : 

.

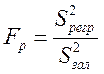При рівні значущості   α = 0,05 знаходимо F_кр(α; k-1; n-k),

де k – кількість параметрів моделі (для лінійної залежності k=2); n – кількість випробувань (у нашому випадку n = 10). 

Для нашого випадку  

  F_кр  = FРАСПОБР(0,05; 2-1; 10-2) = 5,3176.

Обчислене  F_р =2948. Оскільки   F_р > F_кр – модель адекватна.

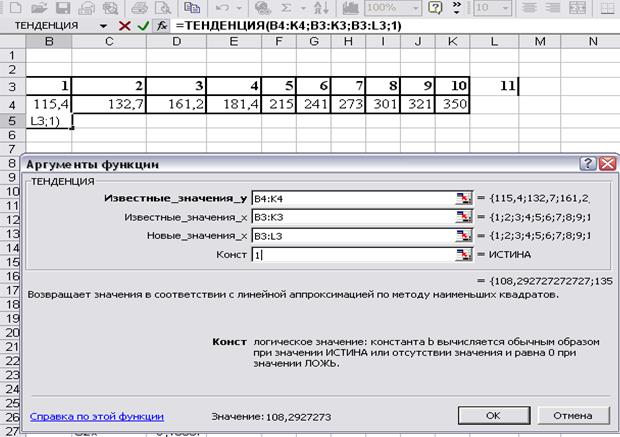
7  Використовуючи функцію ТЕНДЕНЦИЯ,  одержати прогноз величини прибутку на наступний рік.

Виділимо діапазон В5:L5, і скористаємося функцією ТЕНДЕНЦИЯ, як зазначено на малюнку. Після того, як всі параметри введені, необхідно натиснути CTRL+Shift+Enter.

x	1	2	3	4	5	6	7	8	9	10	11
y	115.4	132.7	161.2	181	215	241	273	301	321	350.4
yлін	108.3	135.2	162.0	189	216	243	269	296	323	350.0	376.9

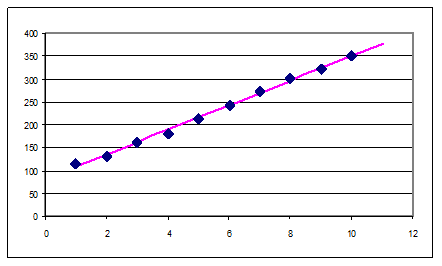
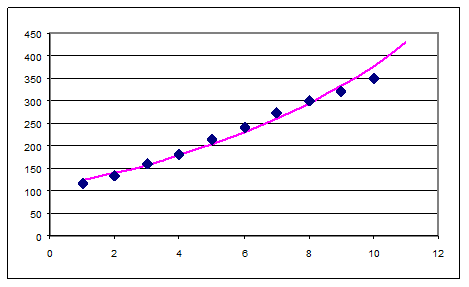
Прогноз при х=11, у=376,9.  Будуємо графік.

8 Знайдемо параметри  регресії , використовуючи функцію ЛГРФПРИБЛ. Параметри вводяться так само, як для функції ЛИНЕЙН. Отримуємо такі дані:

	a1	a0
ai	1.13	108.205
σai=	0.0059095	0.03667
R2, Sig	0.9825	0.05368
Fр, df	448.07	8
SSreg, SSзал	1.290	0.02305

  За результатами обчислень  рівняння регресії =108.205* 1.13^х , коефіцієнт детермінації   =0,9825, отже,  дана залежність описує вхідні дані гірше, ніж лінійна.

9   Розрахувати прогнозоване  значення на кінець наступного року для рівняння регресії =108.205* 1.13^х . Використовуємо функцію РОСТ. Параметри вводяться так само, як для функції ТЕНДЕНЦИЯ.

x	1	2	3	4	5	6	7	8	9	10	11
y	115.4	132.7	161.2	181	215	241	273	301	321	350.4
Урегр	122.62	138.96	157.48	178	202	229	260	294	334	378.02	428.4

Отже, в даному випадку прогноз при х=11 складає 428,4%.

Будуємо графік для функції регресії =108,205*1,13^х.

 

7.9 Парна регресія в матричній формі

Нехай є вибірка з n спостережень (x₁, y₁), (x₂, y₂), ..., (x_n, y_n) для змінних Y і Х.  Рівняння регресії шукаємо у вигляді

,   i = 1, 2, ..., n   (7.9)

або в розгорнутому вигляді

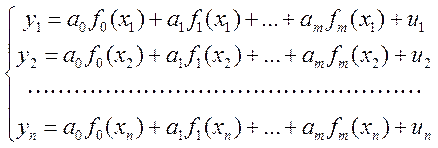 .       (7.10)

Розглянемо вектори-стовпці

,  ,

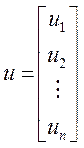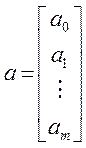
і матрицю розмірності n (m+1):

.

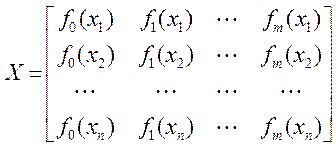Тоді, відповідно до правил множення й додавання матриць, матричний запис системи рівнянь (7.10) набуває вигляду

.                                        (7.11)

Припустимо, що n > m+1, тобто число спостережень перевищує число параметрів моделі.  У  протилежному  випадку  неможлива  оцінка  параметрів.  Вважаємо також, що функції f₀(x)=1, f₁(x), ..., f_m (x) - лінійно незалежні. У цьому випадку ранг (число лінійно незалежних рядків або стовпців) матриці дорівнюєm+1.

Ранг транспонованої матриці        

такождорівнюєm+1, причому її розмірність (m+1)n . Добуток матриць   і    є  симетрична матриця розмірності (m+1)´(m+1):

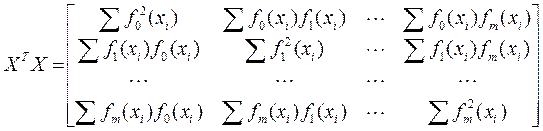      (7.12)

Її ранг дорівнює m+1, тобто визначник  Це означає, що матриця  є невиродженою,  отже, існує обернена матриця , що відіграє основну роль у процедурі оцінювання.