Регресійний аналіз (лінійний) - статистичний метод дослідження залежності між залежною змінною Y і однією або декількома незалежними змінними X1, X2, ..., Xp. Незалежні змінні інакше називають регресорами або предикторами, а залежні змінні - критеріальними.
Регресійний аналіз використовується для визначення загального вигляду рівняння регресії (найчастіше використовується лінійна модель), оцінки параметрів цього рівняння, а також перевірки різних статистичних гіпотез щодо регресії.
Регресійний аналіз має ту ж саму мету, що й кореляційний аналіз – виміряти величину зв'язку між змінними.
Відмінності регресійного аналізу від кореляційного аналізу:
· регресійний аналіз дає можливість графічно представити результат у вигляді лінії (regressio - лат.), що прагне максимально точно відобразити залежність однієї змінної від інших;
· кореляційний аналіз залишає без уваги, навіть формально, питання щодо причинно-наслідкових зв'язків між змінними. Регресійний аналіз припускає, що до початку аналізу відома одна залежна змінна, на яку можуть впливати інші;
· у рамках регресійного аналізу має сенс поняття прогнозування значень залежної змінної від незалежних.
Всі методи регресійного аналізу використовують апарат математичної статистики, що вимагає від вхідних даних, щоб вони були порівнянні і однорідні. Для виявлення закономірностей необхідно, щоб зв'язок був стійкий, а кількість спостережень була досить великою.
Порівнянність: формування вибірок за однією й тією ж методикою, використання однакових одиниць виміру і, по можливості, постійного кроку спостереження.
Однорідність: відсутність сильних зломів і нетипових аномальних спостережень (різкий стрибок з подальшим відновленням).
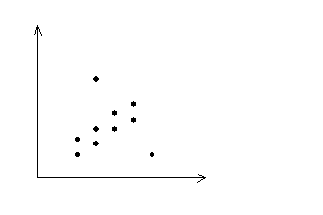
Стійкість: перевага закономірності над випадковістю. Графік діаграми дозволяє провести візуальний аналіз даних.
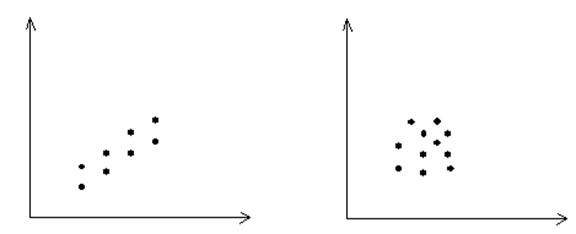
(точки розташовані у вигляді (точки розкидані)
вузької смуги)
Розглянемо основні передумови регресійної моделі.
І припущення полягає в тому, що між змінними Х та Y постулюється зв'язок
, тобто виконана ідентифікація
змінної Х, що впливає на змінну Y.
Парна регресія встановлює зв'язок однієї випадкової величини від іншої.
Множинна регресія встановлює зв'язок однієї випадкової величини від декількох випадкових змінних.
Ця залежність є статистичною, оскільки, крім виділеної змінної X, на Y діє ряд неконтрольованих факторів, а також накладаються похибки вимірювань.
Значення залежної змінної піддані випадковому розсіюванню і можуть бути передбачені тільки з певною ймовірністю.
Статистична залежність є однобічною. Тому розрізняють регресію X на Y і Y на X .
Для
функціональної залежності може існувати обернена функція (
обернена 
).
Регресія такої властивості не має.
У класичній регресійній моделі припускають, що значення змінної X є невипадковими величинами. Вони або фіксовані (як, наприклад, у часових рядах моменти часу t1, t2, ..., tn), або керовані (контрольовані). В останньому випадку реалізацію у випадкової змінної Y називають реакцією системи на керування. Типовий приклад: незалежна змінна являє собою кількість добрив, внесених на поле (керування), а залежною змінною служить розмір урожаю, зібраного на цьому полі (відгук). Таке допущення дозволяє замість зіставлення двох випадкових величин Y і X вести мову про залежність випадкової величини Y від невипадкового (керованого) параметра х.
II припущення полягає у специфікації форми зв'язку Y і Х. Оскільки вхідні дані можна описати за допомогою різних типів функцій (лінійної, логарифмічної, поліноміальної та ін.), необхідно за допомогою статистичного аналізу вибрати серед альтернативних варіантів «кращий».
У випадку парної регресії
,
де a0 ,a1,..am – невідомі параметри.
Позначка ˇ означає, що між x і y існує статистичний зв'язок.
Рівняння регресії знаходять за емпіричними даними, що містять випадковості й впливи вторинних причин, які своєю мінливістю спотворюють істинний зв'язок.
Величину
називають збурюванням. Вона
характеризує відхилення змінної Y від величини
, обчисленої за функцією регресії.
Тоді випадкову величину Y можна представити у вигляді
,
де a0 ,…, am – невизначені коефіцієнти.
U – враховує невраховані фактори, похибки спостереження, а також її можна інтерпретувати як випадкову змінну, що враховує неправильний вибір форми рівняння.
Визначити значення U можна тільки після кількісної оцінки функції регресії.
III припущенняполягає в можливості оцінювання параметрів a0 , …, am.
Класичний регресійний аналіз оцінок параметрів a0 ,…, am базується на методі найменших квадратів, що встановлює обмеження на вигляд функції регресії.
1 Параметри a0, …, am та збурювання U повинні входити до функції регресії лінійно:
.
2 Якщо обрано нелінійну модель, то передбачається, що й збурювання U входить у неї нелінійно:
, (7.1)
і повинне існувати перетворення рівняння (7.1) таке, що:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
