де di 2= (xi–yi)2 – квадрати різниць рангів;
n – кількість спостережень.
Коефіцієнт Спірмена приймає значення з інтервалу [-1;1].
Для нашого прикладу
|
X |
1 |
2 |
3 |
4 |
5 |
|
|
Y |
4 |
1 |
2 |
5 |
3 |
|
|
di |
-3 |
1 |
1 |
-1 |
2 |
|
|
di 2 |
9 |
1 |
1 |
1 |
4 |
|
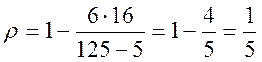 =0,2.
=0,2.
Зв'язок між ознаками вважається статистично значущим, якщо значення коефіцієнтів рангової кореляції Спірмена і Кенделла більше 0,5.
Для нашого прикладу
коефіцієнт Кенделла τ =0,2, коефіцієнт рангової кореляції Спірмена ![]() , що свідчить про практичну відсутність зв'язку між розглянутими ознаками
X та Y.
, що свідчить про практичну відсутність зв'язку між розглянутими ознаками
X та Y.
Як правило, коефіцієнт Кенделла менший коефіцієнта Спірмена. При досить великому обсязі сукупності значення даних коефіцієнтів мають таку залежність:
t=2/3 ρ
Коефіцієнт Спірмена (ρ) – легше розраховувати, але з теоретичної точки зору коефіцієнт Кенделла (τ) становить більший інтерес.
Якщо не можна встановити рангове розходження між декількома об'єктами,
їх називають зв'язаними. В цьому випадку об’єктам приписують
середній ранг. Наприклад, якщо об'єкти 4,5,6 – мають однакові значення, то їх
середній ранг дорівнює (4+5+6)/3=5. Сума рангів зв’язаних об’єктів повинна
дорівнювати сумі рангів при ранжуванні без урахування
зв’язків.
Якщо t послідовних членів Х зв'язані, то всі оцінки, що відносяться до будь-якої пари, що вибрані з них, дорівнюють нулю. Число таких пар t(t – 1). Тоді
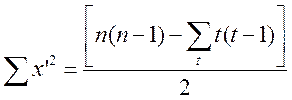 .
.
Відповідно для другої послідовності Y
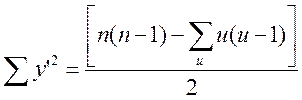 ,
,
де t та u – кількість зв’язаних пар у послідовностях. Позначимо
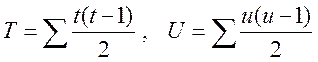 .
.
Отримаємо вираз для розрахунку коефіцієнта Кенделла при наявності зв’язаних об’єктів
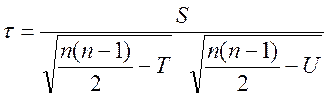 . (9.4)
. (9.4)
Аналогічно знаходимо вираз для обчислення коефіцієнта Спірмена. Тільки в цьому випадку
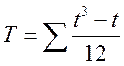 ,
, 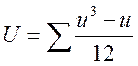 .
.
Отримаємо вираз для розрахунку коефіцієнта Спірмена при наявності зв’язаних об’єктів
 . (9.5)
. (9.5)
Приклад. На змаганнях з фігурного катання судді таким чином розташували учасників змагань:
|
учасники |
||||||||||
|
А |
Б |
В |
Г |
Д |
Є |
Ж |
З |
І |
К |
|
|
1 суддя |
1,5 |
1,5 |
3 |
4 |
6 |
6 |
6 |
8 |
9,5 |
9,5 |
|
2 суддя |
1 |
2 |
4 |
4 |
4 |
6 |
7 |
8 |
9 |
10 |
Встановити, наскільки об’єктивні оцінки суддів, тобто на скільки тісний зв'язок між їхнім оцінками. Обчислити коефіцієнти рангової кореляції Спірмена та Кенделла.
Розв’язок.
За думкою першого судді учасники А і Б поділили перше місце, тому їх об’єднаний ранг дорівнює (1+2)/2=1,5. Учасники Д, Є, Ж поділили 5,6,7-е місця, отже їх об’єднаний ранг дорівнює (5+6+7)/3=6, учасники І, К поділили 9,10-е місця, отже їх об’єднаний ранг дорівнює (9+10)/2=9,5. При обчисленні Т маємо: А і Б – два об’єднаних ранги; Д, Є, Ж – три об’єднаних ранги; І, К – два об’єднаних ранги. Для другого судді маємо: В, Г, Д – три об’єднаних ранги.
Обчислимо ранговий коефіцієнт Спірмена. Для цього спочатку обчислимо ![]() .
.
|
учасники |
||||||||||
|
А |
Б |
В |
Г |
Д |
Є |
Ж |
З |
І |
К |
|
|
1 суддя |
1,5 |
1,5 |
3 |
4 |
6 |
6 |
6 |
8 |
9,5 |
9,5 |
|
2 суддя |
1 |
2 |
4 |
4 |
4 |
6 |
7 |
8 |
9 |
10 |
|
d2 |
0,25 |
0,25 |
1 |
0 |
4 |
0 |
1 |
0 |
0,25 |
0,25 |
![]() .
.
Потім обчислимо значення Т і U:
Т=[(22 – 2) + (33 – 3) + (22 – 2)]/12=3,
U= (33 – 3)/12=2.
За формулою
 ,
,
де n – кількість спостережень (для нашого випадку n=10), знаходимо
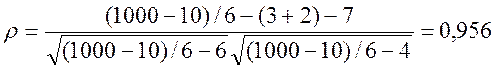 .
.
Обчислимо коефіцієнт кореляції рангів Кенделла за формулою
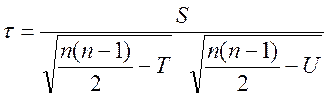
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.