Фактичне значення частки F–критерію порівнюється з табличним при рівні значущості α та кількості ступенів вільності k1= 1 та k2=n-m-1. Якщо фактичне значення Fxi перевищує Fkp(α; k1; k2), то додаткове включення фактора xi в модель статистично виправдане і коефіцієнт регресії аі при факторі xi статистично значущий. Якщо ж фактичне значення Fxi менше табличного, то додаткове включення в модель фактора xi не збільшує істотно частку поясненої варіації ознаки Y, отже, недоцільне його включення в модель; коефіцієнт регресії при даному факторі в цьому випадку статистично незначущий.
Кроковий регресійний метод діє у зворотному порядку порівняно з методом виключень. Фактори по черзі включаються в модель до того часу, поки вона не стане задовільною. Порядок включення вибирається за допомогою коефіцієнта кореляції як міри важливості факторів (незалежних змінних), які ще не включені в модель. Кроковий регресійний метод також зручно подати у вигляді узагальненого алгоритму, що умовно розіб'ємо на три етапи.
Алгоритм методу:
1 Спочатку
обирається фактор ![]() ,
що має найбільший коефіцієнт кореляції з Y (нехай це буде змінна Х1).
Будується регресійне рівняння з однією незалежною змінною
,
що має найбільший коефіцієнт кореляції з Y (нехай це буде змінна Х1).
Будується регресійне рівняння з однією незалежною змінною ![]() . Після цього перевіряємо, чи значуща вона
за частковим F-критерієм. Якщо ні, то приймаємо
. Після цього перевіряємо, чи значуща вона
за частковим F-критерієм. Якщо ні, то приймаємо ![]() і припиняємо процес. Якщо так, то шукаємо
другу змінну, що має найменший коефіцієнт кореляції з Y, яку варто включити в модель. Нехай це
буде змінна X2.
і припиняємо процес. Якщо так, то шукаємо
другу змінну, що має найменший коефіцієнт кореляції з Y, яку варто включити в модель. Нехай це
буде змінна X2.
2 Будується нове рівняння регресії
![]() .
.
Аналізується зміна коефіцієнта кореляції R2 тa розраховуються часткові F-критерії для кожного фактора. Серед них обирається найменше його значення й порівнюється із заздалегідь вибраним критичним значенням F-розподілу. Відповідно до результатів перевірки змінна або залишається в моделі, або відкидається.
Може відбутися так, що фактор, який на певному із етапів був найкращим для включення, потім з моделі вилучається.
3 Після цього модель перераховується залежно від факторів, які залишилися.
Варто відмітити, що на першому етапі, крім перевірки за коефіцієнтом кореляції, фактор-претендент на включення може перевірятися також за частковим F-критерієм. Якщо він відповідає йому, то фактор включають у модель, якщо ні, то переходять до аналізу наступного фактора.
Процес побудови моделі припиняється, якщо ніякий фактор, що знаходиться в поточному рівнянні, не вдається виключити, а новий претендент на включення не відповідає частковому F-критерію. Кроковий метод є найпоширенішим на практиці.
1 Що являє собою регресійний аналіз? Його призначення.
2 Чим відрізняється регресійний аналіз від кореляційного?
3 Вимоги до параметрів регресійного аналізу.
4 Припущення, які використовує регресійний аналіз.
5 Метод Фостера – Стюарта, його суть.
6 Вибір виду функції для монотонних процесів.
7 Суть методу найменших квадратів.
8 Властивості регресії.
9 Коефіцієнт детермінації, його суть та формули для обчислення.
10 Індекс та коефіцієнт кореляції, їх відмінності.
11 Критерій Фішера.
12 Функції Excel для побудови регресійних залежностей.
13 Парна регресія.
14 Множинний регресійний аналіз.
15 Перевірка значущості коефіцієнтів регресії.
16 Парна й часткова кореляції.
17 Методи побудови багатофакторної регресійної моделі.
18 Покажіть, що величина вибіркового коефіцієнта кореляції r не залежить від одиниць виміру змінних.
19 Знайдіть перетворення даних, яке зводить дану модель до лінійної. Визначте, яким чином потрібно включити збурення до моделі:
1)![]() 2)
2)![]() 3)
3)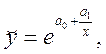
4)
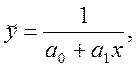 5)
5) 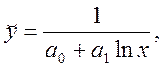 6)
6)
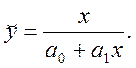
20 Спостереження 16
пар (xi, yi) дали такі результати: Σyi2=526, Σ хi2= 657, Σxiyi=492, Σ yi =64, Σxi=96. Знайдіть параметри регресії ![]() =a0+a1x.
=a0+a1x.
21 При побудові
регресії ![]() =a0+a1x за 15 спостереженнями отримали, що Σ(
=a0+a1x за 15 спостереженнями отримали, що Σ(![]() )2=10, Σ(
)2=10, Σ(![]() )2=277, Σ(
)2=277, Σ(![]() )2=287.
)2=287.
Обчислити коефіцієнт детермінації, оцінити якість моделі. Перевірити модель на адекватність при 1 % рівні значущості.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.