Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 5

am	…....	a1	a0
san		sa1	sa0
R2	sy
F	df
SSreg	SSзал

a_m ,…, a_1, a₀ – коефіцієнти рівняння регресії;

s_ai – похибки обчислення для коефіцієнтів;

R² –  коефіцієнт детермінації й s_у - похибки обчислення для  y;

F – статистика  (F розраховане) і df - кількість ступенів вільності;

SSreg – регресійна сума квадратів; SSзал – залишкова сума квадратів.

Функція ТЕНДЕНЦИЯ повертає значення відповідно до лінійного тренда. Вона за методом найменших квадратів апроксимує прямою лінією масиви <відомі_значення_y> і <відомі_значення_x>. Повертає значення y відповідно до цієї прямої для даного заданого масиву <нові_значення_х>.

ТЕНДЕНЦИЯ (відомі_значення_у; відомі_значення_х; нові_значення_х; константа). Значення Константа обирається відповідно до вигляду функції регресії так само, як і для функції Линейн.

ЛГРФПРИБЛ(відомі_значення_у; відомі_значення_х;

нові_значення_х; конст; статистика).

ЛГРФПРИБЛ – рівняння кривої таке: , де залежне значення Y є функцією незалежних значень х. Значення a₁ є підставою для піднесення до степеня х, а значення a₀ постійне. Відмітимо, що y, x і a можуть бути векторами. Функція ЛГРФПРИБЛ повертає масив{a_n; a_n-1;...;a₁, a₀}. Параметри та результати обчислень функції ЛГРФПРИБЛ за змістом співпадають з відповідними даними функції  Линейн.

Функція РОСТ повертає значення у для послідовності нових значень х, що задаються за допомогою існуючих х- і у-значень. Функція РОСТ може застосовуватися також для апроксимації існуючих х- і у-значень експонентною кривою.

Приклад. У таблиці  7.2 наведена динаміка зростання прибутку деякої фірми за останні n років у відсотках до базового року.

1  Побудувати діаграму. Оцінити за нею вигляд залежності.

2  Обчислити коефіцієнти коваріації й лінійної кореляції. Зробити висновки.

3  Розрахувати а₀ і а₁ для  лінійної регресії =a₀+a₁x, використовуючи коефіцієнт  лінійної кореляції. Записати отримане рівняння.

4  Перевірити свої розрахунки, використовуючи функцію ЛИНЕЙН.

5  Знайти коефіцієнт детермінації.

6  Оцінити адекватність моделі за критерієм Фішера при рівні значущості   α = 0,05.

7  Використовуючи функцію ТЕНДЕНЦИЯ, одержати прогноз величини прибутку на наступний рік.  Побудувати графік.

8  Використовуючи функцію ЛГРФПРИБЛ, одержати рівняння кривої.

9   Порівняти коефіцієнти детермінації для лінійної та експонентної залежностей.

10  Розрахувати прогнозоване  експонентне зростання на підставі наявних даних.

Таблиця  7.2 – Динаміка зростання прибутку фірми за останні 10 років у відсотках до базового року

Рік	1	2	3	4	5	6	7	8	9	10
Прибуток	115.4	132.7	161.2	181.4	214.5	241.2	272.9	301.4	320.5	350.4

Розв’язання

1 Побудуємо діаграму за вхідними даними:

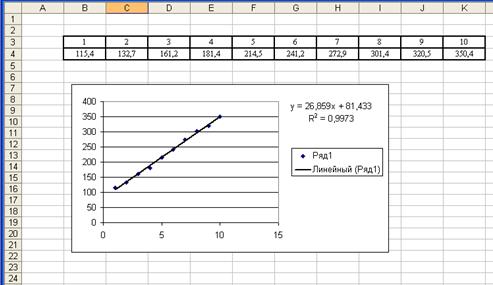
Легко помітити, що дані наближено мають лінійну залежність.

2 Обчислимо коваріацію й коефіцієнт кореляції

cov(x,y)= 221,59 –  пряма залежність між Х і У;

=0,99865– яскраво виражена лінійна залежність.

3  Розрахункові формули для коефіцієнта лінійної регресії :

 =  = ;       = .

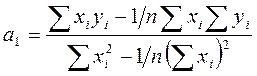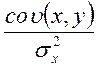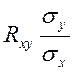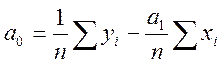	5,5	СРЗНАЧ(B3:K3)
	229,16	СРЗНАЧ(B4:K4)
σx=	2,872281	СТАНДОТКЛОНП(B3:K3)
σy=	77,25236	СТАНДОТКЛОНП(B4:K4)

a₁= 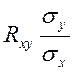=26,859;     a₀  = =81,433.

Отже, отримане рівняння       =26.859x + 81.433.

4 Перевірити свої розрахунки, використовуючи функцію ЛИНЕЙН.