Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 13

Метод усіх можливих регресій був історично першим методом побудови регресійної моделі. Він дуже громіздкий і може бути реалізований лише на ЕОМ.

Метод вимагає побудови всіх можливих регресійних рівнянь, які обов'язково включають член  β₀. Оскільки для кожного фактора Х_і є дві можливості – входити  або не входити в регресію, то всього буде 2p рівнянь (де  р - кількість факторів  X_i, i=1,p).  Розглянемо ідею цього методу на прикладі лінійної регресійної моделі з 4 факторами:  X₁, X₂, X₃, X₄. При цьому будемо мати 2⁴=16 всіх можливих рівнянь, які розіб'ємо на 5 серій:

І серія моделей включає тільки один випадок:

ІІ серія – всі можливі однофакторні рівняння, у нашому випадку їх чотири:

ІІІ серія – всі можливі двофакторні моделі.

ІV серія – всі трьохфакторні моделі.

V серія – всі чотирьохфакторні моделі. Це буде, як і в І серії, одна модель:

Після того як ми розбили всі моделі за серіями, проранжуємо їх усередині кожної серії за значенням R² (обмежимося розглядом тільки критерію R²). Виявимо моделі, які мають найбільше значення коефіцієнта детермінації   в кожній із серій, і проаналізуємо,  чи є якась закономірність у змінних, які входять у кожне з "найкращих" рівнянь. Вибір остаточного рівняння – це деякою мірою суб'єктивна оцінка дослідника.

Якщо для певної задачі побудовані всі регресійні рівняння, то, розглядаючи залежність величини середнього квадрата залишків від числа змінних р, іноді можна найкращим способом вибрати кількість змінних, які необхідно зберегти в регресійній моделі. Якщо ми до такої моделі будемо додавати все нові й нові фактори, середній квадрат залишків буде стабілізуватися й наближатися до дисперсії залишків σ_ε2 (за умови, що найважливіші змінні увійшли в модель, а кількість факторів у 5-6   разів перевищує кількість спостережень).

З одного боку, метод  аналізу всіх можливих рівнянь регресії дає можливість розглянути й дослідити всі можливі рівняння, але, з іншого боку, при великій кількості факторів це призводить до більших витрат машинного часу, збільшення тривалості аналізу, можливих помилок і т. ін. Виходячи із цього, метод всіх можливих рівнянь краще використовувати при невеликій кількості факторів, які входять у модель.

7.12.3 Метод виключень

Цей метод більш економічний, ніж метод всіх регресій. Загальний алгоритм методу складається з 5 етапів.

1    На першому етапі розраховується регресійне рівняння, що включає всі фактори, які входять у модель. Якщо було відібрано  р факторів, то базове регресійне рівняння має вигляд

 

2    На другому етапі обчислюється величина часткового F-критерію для кожного фактора.

3    Менше значення часткового F-критерію, що порівнюється із заздалегідь вибраним критичним значенням F_kp, позначається F_l.

4    Якщо F_l < F_kp , то відповідний фактор виключається з рівняння. Проводиться новий розрахунок регресійного рівняння вже без цього виключеного фактора й знову переходять до етапу 2.

5    Якщо F_l > F_kp, то регресійне рівняння залишають без змін.

У статистиці метод виключень є досить поширеним, оскільки дозволяє відразу побачити всі фактори в моделі.

У деяких комп'ютерних програмах замість часткового F-критерію використовується t-критерій, що є коренем квадратним від значення часткового F-критерію. Крім того, іноді використовується термін "F–критерій для виключення", ідентичний терміну "частковий F–критерій".

Частковий F–критерій побудований на порівнянні приросту факторної дисперсії, обумовленої впливом додатково включеного фактору, із залишковою дисперсією на один ступінь волі по регресійній моделі в цілому. У загальному вигляді для фактору x_i частковий F–критерій визначається як

,

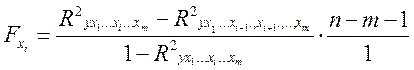де  – коефіцієнт множинної детермінації для моделі з повним набором факторів,  – той же показник, але без включення в модель факторуx_i, n– число спостережень, m– число параметрів  моделі (без вільного члена).