Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 8

										суми
x	1	2	3	4	5	6	7	8	9	45
y	35,4	34,2	33,6	32,1	32,7	33,8	35,6	37,2	38,8	313,4
x2	1	4	9	16	25	36	49	64	81	285
X3	1	8	27	64	125	216	343	512	729	2025
X4	1	16	81	256	625	1296	2401	4096	6561	15333
yx	35,4	68,4	100,8	128,4	163,5	202,8	249,2	297,6	349,2	1595,3
yx2	35,4	136,8	302,4	513,6	817,5	1216,8	1744,4	2380,8	3142,8	10290,5

.

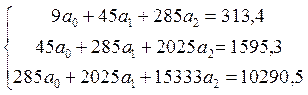Тепер у нас є система трьох рівнянь із трьома невідомими.

Подамо цю систему в матричній формі AX=B, де X=(a0, a1, a2).

	9	45	285
A	45	285	2025
	285	2025	15333

	313,4
B	1595,3
	10290,5

Перевірку сумісності системи можна виконати, обчисливши визначник матриці А за допомогою функції EXCEL МОПРЕД(<діапазон>).

Розв’язок визначаємо матричним методом за формулою X= A^-1B, обернена матриця A^-1 обчислюється за допомогою функції Excel  МОБР(<діапазон>).

A-1	1,619048	-0,67857	0,059524
	-0,67857	0,341342	-0,03247
	0,059524	-0,03247	0,003247

Добуток матриць A^-1B обчислюється за допомогою функції ExcelМУМНОЖ(<матриця 1>;< матриця 2>). Одержуємо коефіцієнти регресії

a0=	37,4142857
a1=	-2,2285498
a2=	0,27002165

Отже, рівняння регресії має вигляд

37, 414-2,229x+0,270x².

Визначення невідомих параметрів регресії (а₀ , а₁ , а₂)  матричним способом.

Матричний запис системи для визначення параметрів регресії такий:             .     

Запишемо матриці X таY.

	1	1	1	35,4		35,4
	1	2	4	34,2		34,2
	1	3	9	33,6		33,6
X	1	4	16	32,1	Y	32,1
	1	5	25	32,7		32,7
	1	6	36	33,8		33,8
	1	7	49	35,6		35,6
	1	8	64	37,2		37,2
	1	9	81	38,8		38,8

Обчислимо X^Т за допомого функції Excel ТРАНСП(<масив>).

XТ	1	1	1	1	1	1	1	1	1
	1	2	3	4	5	6	7	8	9
	1	4	9	16	25	36	49	64	81

Обчислимо добутки матриць X^ТХ та X^ТY (функція Excel МУМНОЖ(<матриця 1>;< матриця 2>).

	9	45	285		XТY	313,4
XТХ	45	285	2025			1595,3
	285	2025	15333			10290,5