Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 10

,

тут  – фіктивна змінна, яка введена для зручності;

U – відображає вплив на Y інших факторів, помилки вимірювань, помилки вибору моделі.

Виникають такі задачі:

1   Знайти за даними спостережень вибіркове рівняння зв'язку

,

тобто знайти коефіцієнти регресії.

2   Оцінити тісноту зв'язку між Y і  X_i, , а також між X_i та  X_j .

3   Оцінити тісноту зв'язку між Y і  X_i при постійних X_j ().

Перша задача розв’язується методом найменших квадратів. Критерієм вибору оцінок  є умова мінімуму суми квадратів відхилень .

.

Умовою досягнення екстремуму є рівність нулю часткових похідних

,     ,  ... , .

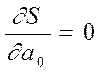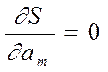Одержуємо систему  m+1 лінійних рівнянь із m+1 невідомими:

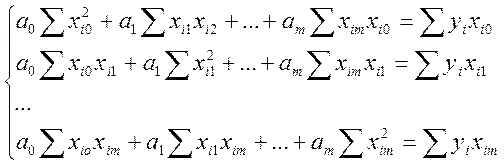.    (7.16)

Якщо n> m-1 і визначник системи  знаходимо єдиний розв’язок системи .

7.11.1 Матричний спосіб оцінки параметрів множинної регресії

Розглянемо вектори-стовпці

,  ,

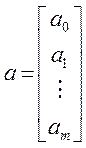
і матрицю  Х розмірності n (m+1):

.

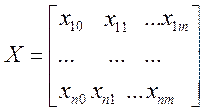Тоді відповідно до правил множення й додавання матриць матричний запис системи рівнянь (7.16) набуває вигляду

.                                       

де  – транспонована матриця Х. Добуток матриць Х^ТХ дорівнює

.

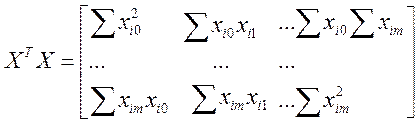Матриця Х^ТХ  має розмірність (m+1) (m+1).

Якщо n> m-1 і ранг матриці Х^ТХ дорівнює m+1 , система має єдиний розв’язок 

.

7.11.2 Перевірка значущості коефіцієнтів регресії

Для цього застосовуємо  t–критерій Стьюдента, за допомогою якого перевіряють, чи значуще a_i відрізняється від нуля. Висуваємо гіпотези:

Н₀: ;      Н₁: ;

Обчислюємо критеріальне значення

.

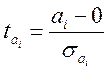Обчислюємо критичне значення  

,

де k – кількість параметрів регресії. Якщо  – a_i  статистично незначуще відрізняється від нуля, а якщо  –  a_i  статистично значуще.

Якщо виникає ситуація, що a_i  статистично незначуще відрізняється від нуля, то це означає, що вплив i-го фактора на досліджувану змінну нестабільний.

7.11.3 Перевірка якості моделі. Скоригований коефіцієнт детермінації

Якість моделі характеризується коефіцієнтом детермінації

             .       

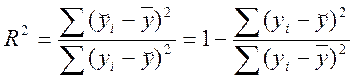Коефіцієнт детермінації як критерій вибору функції регресії має суттєвий недолік, що полягає в тому, що з додаванням до регресії нових змінних він ніколи не зменшується, а, навпаки, збільшується. Це означає, що рівняння з більшим числом регресорів буде давати кращі результати, ніж з відносно малою їх кількістю. Але з додаванням нового фактора губиться один ступінь вільності, що не завжди бажано. Наприклад, довірчі інтервали будуть тим менші, чим більше число ступенів вільності L= n-m-1. При застосуванні критеріїв Стьюдента  й Фішера також бажано мати можливо більше число ступенів вільності.

Скоригований коефіцієнт детермінації з виправленням на число ступенів вільності визначається

.

Для перевірки адекватності моделі розраховуємо критеріальне значення

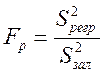
та критичне значення

,

де , ,

 k – кількість параметрів моделі; n – кількість спостережень. Значення F_кр обчислюємо за допомогою функції FРАСПОБР(α; k-1; n-k).  Якщо F_p>F_kp  –  модель адекватна.

7.11.4 Парна й часткова кореляції

Вибіркові коефіцієнти парної кореляції обчислюються за формулою

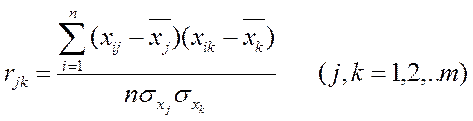
Виникає питання: спостережувана кореляція змінної (Y) і якої-небудь незалежної змінної (Х₁) обумовлена чистою залежністю між ними або інша змінна (Х₂) впливає на них, що стає причиною спостережуваної кореляції між Y і X₁. Таким чином, ми приходимо до поняття часткової кореляції між Y і X₁, коли вплив X₂ усунуто.

Часткові коефіцієнти кореляції обчислюються у такий спосіб:

.

В економетриці часткові коефіцієнти кореляції звичайно не мають самостійного значення. Їх використовують на стадії формування моделі. Так, будуючи багатофакторну модель, на першому кроці визначається рівняння регресії з повним набором факторів, і розраховується матриця часткових коефіцієнтів кореляції. На другому кроці відбирається фактор з найменшої й несуттєвої за - критерієм Стьюдента величиною показника часткової кореляції. Виключивши його з моделі, будується нове рівняння регресії. Процедура триває до того часу, поки не виявиться, що всі часткові коефіцієнти кореляції істотно відрізняються від нуля. Якщо виключено несуттєвий фактор, то множинні коефіцієнти детермінації на двох суміжних кроках побудови регресійної моделі майже не відрізняються один від одного, , де m – число факторів.