Математика \ Математическая статистика

Аналіз даних: Навчальний посібник (Розділи: Регресійний аналіз. Дисперсійний аналіз. Ранговий аналіз), страница 22

Для обчислення коефіцієнта Кенделла  необхідно знайти значення S, тобто . Якщо i=j, то =0 (або =0).

Заповнимо таблицю для розрахунку S.

А

Б

В

Г

x′

y′

x′ y′

x′

y′

x′ y′

x′

y′

x′ y′

x′

y′

x′ y′

0

1

0

1

1

1

1

0

0

1

0

0

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

Σ5

1

1

1

1

1

1

Σ5

1

1

1

Σ8

Σ8

Д

Є

Ж

З

І

x′

y′

x′ y′

x′

y′

x′ y′

x′

y′

x′ y′

x′

y′

x′ y′

x′

y′

x′ y′

0

1

0

0

1

0

1

1

1

1

1

1

0

1

0

0

1

0

1

1

1

1

1

1

1

1

1

Σ2

1

1

1

1

1

1

1

1

1

Σ2

1

1

1

1

1

1

Σ3

1

1

1

Σ3

Σ3

Далі знаходимо:

S=(8+8+5+5+3+3+3+2+0)= 37,

,

.

Отже коефіцієнта кореляції рангів Кенделла   дорівнює

.

Можна зробити висновок, що оцінки, виставлені суддями учасникам змагань, об’єктивні,  оскільки обидва коефіцієнти близькі до 1.

9.3 Коефіцієнт конкордації

Нехай m експертів ранжують n факторів. Кожному фактору кожний експерт присвоює ранг – ціле число від 1 до n, приписуючи ранг 1 найбільш важливому фактору, ранг 2 – наступний по важливості і т.д. На підставі цих даних складається матриця рангів

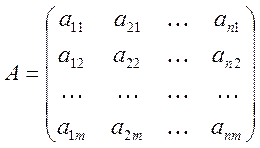,                           (9.6)

де - ранг j-го фактору ( ), визначений i-м експертом ( ), номери рядків відповідають номерам експертів, а номери стовпців – номерам факторів. Це означає, що i-й рядок являє собою думку i-го експерта про усі фактори, а j-й стовпець – думка усіх експертів з приводу j-го фактора.

На базі даних матриці (9.6) обчислюємо:

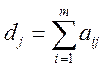 – сума рангів j-го фактора ();

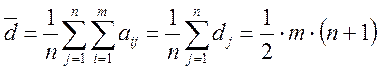 – середнє значення усіх рангів; 

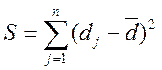 – сума квадратів відхилень від середнього для кожного з факторів.

Скачать файл