Отчет о научно-исследовательской работе "Развитие проекта «ТЭО берегоукрепления восточной части Финского залива». Исследование гидрологического режима в прибрежной зоне Курортного района Санкт-Петербурга", страница 4

Методика оценки пространственных радиусов корреляции основывается на разработанном программном модуле объективного анализа пространственных данных и включает в себя определение величин анизотропных радиусов корреляции в двух направлениях: c севера на юг и с запада на восток. Выявленная таким образом геометрическая анизотропия дополняется определением параметров физической неоднородности (пространственной дисперсии поля). Минимальные значения величин полуосей определенных таким образом эллипсов влияния для всех анализируемых параметров могут быть интерпретированы как максимальные расстояния между станциями и разрезами оптимальной сети наблюдений экологического мониторинга.

Учитывая большую изменчивость физических процессов, протекающих в мелководных районах, к которым можно отнести как Невскую губу, так и фактически всю восточную акваторию залива, были проведены оценки величин пространственной корреляции для данных, априорно относящихся к двум различным районам Невской губы. Результаты расчетов параметров вариограммы для CTD-съемки поля температуры для районов, удаленных друг от друга на расстояние порядка 4-5 км, представлены в таблице 1.1. Здесь и далее верхняя строка таблицы представляет результаты изотропного анализа, нижняя – анизотропного.

Таблица.1.1.

Параметры эмпирической вариограммы поля  поверхностной температуры

двухполигональной съемки

Очевидно, что интенсивность физических процессов, протекающих в этих двух районах существенно различна. Это приводит к возникновению трехкластерной структуры вариограммы (рисунок 1.2) и, как следствие, переоценке радиусов пространственной взаимосвязи данных.

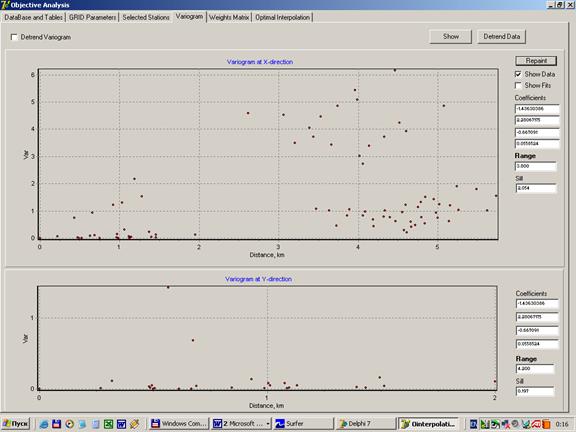
Рисунок  1.2.  Облако точек анизотропной эмпирической вариограммы в направлении восток-запад (верхняя часть) и север-юг (нижняя часть) для поля температуры

на горизонте 0 м.

Более корректный анализ поверхностных данных необходимо проводить для каждого из таких районов отдельно. Результаты такого анализа для области с наибольшей обеспеченностью данными приведены в таблице 1.2.

Таблица 1.2.

Параметры эмпирической вариограммы поля поверхностной температуры

Из таблицы 1.2 видно значимое уменьшение радиуса корреляции, вызванное увеличением однородности исходных данных. Геометрическая анизотропия выражена слабо, что может служить индикатором того, что поле температуры формируется за счет ортогонального вертикального энергообмена, что подтверждает сказанное ранее. Однако следует учесть, что вследствие неоднородности глубин в исследуемой области, прогрев или охлаждение в свою очередь также могут быть неоднородными. Для исключения влияния вариаций донной топографии на анализируемый параметр к исходным данным была применена процедура детрендизации, состоящая в исключении двумерного линейного тренда. Эта процедура обеспечивает исходной информации свойство стационарности второго рода, подразумевающее (как одно из условий) неизменность математического ожидания внутри анализируемого домена. Присутствие в полях наблюдений трендовой крупномасштабной составляющей приводит к завышенной оценке радиусов корреляции и как следствие переоценка максимального шага ОСН.

Таблица 1.3.

Параметры эмпирической вариограммы поля поверхностной температуры с удаленным линейным трендом