Отчет о научно-исследовательской работе "Развитие проекта «ТЭО берегоукрепления восточной части Финского залива». Исследование гидрологического режима в прибрежной зоне Курортного района Санкт-Петербурга", страница 18

Модель перелива через гребень дюны. Рассматриваемая ситуация поясняется рисунком 3.4.

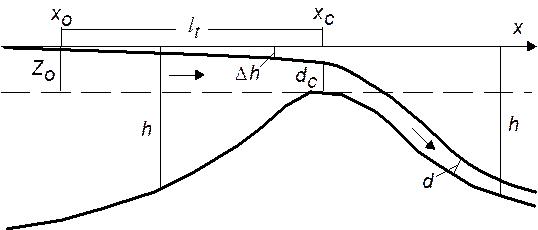
Рисунок 3.4. Схема течения, возникающего при переливе через гребень дюны

Здесь уместна аналогия со случаем водослива с широким порогом, хорошо известным из гидравлики. Над порогом скорость течения достигает критического значения (число Фруда Fr равно 1). Соответственно в точке  скорость , расход воды  и глубина переливного потока  равны

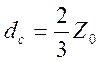,    ,                                                          (3.5)

где  - превышение уровня моря над гребнем дюны.

Из рисунка 3.2 видно, что имеется переходная зона , где уровень воды понижается на величину , причем в точке  , а в точке  . Длина зоны в первом приближении может быть оценена как .

Таким образом, выделяются три области, в которых скорость переливного течения V определяется различным образом:

,                     ,

.    ,                                                                    (3.6)

,                    

В первых двух областях течение действует совместно с волнами, и расход наносов здесь определяется по формуле (3.3). Для этого среднее по сечению значение V пересчитывается в придонное значение  при использовании логарифмического профиля скорости:

,                                                                             (3.7)

где  - кажущаяся донная шероховатость.

В области  волны исчезают, так как их энергия поглощается течением, скорость которого становится выше критической (Fr>1). Основываясь на уравнениях Бернулли и неразрывности, можно принять в первом приближении, что глубина переливного течения уменьшается вниз по склону (с ростом h) как

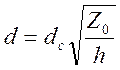                                                                                                 (3.8)

Расход наносов в переливном потоке  оценивается по модифицированной формуле Бэгнольда для поступательного течения [Леонтьев, 2001]

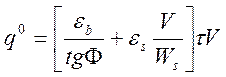,            ,                                       (3.9)

где  - донное касательное напряжение.

Исходные данные

Вид профилей берега, послуживших прототипом при моделировании деформаций, показан на рисунок 3.5.

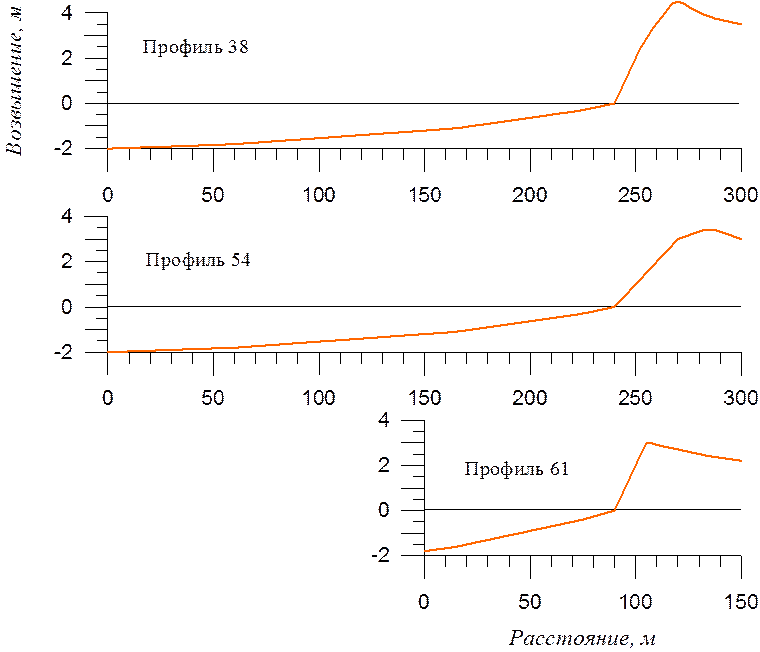
Рисунок 3.5. Береговые профили, использованные при моделировании штормовых деформаций

Подводная часть профилей построена на основе навигационной батиметрической карты и характеризуется уклонами дна порядка 10^-2. Средний размер, плотность и пористость песка при расчетах принимались равными соответственно 0.3 мм,  кг м^-3 и 0.4.

Для характеристики максимальных уровней использовались данные 50 %, 5 % и 1% обеспеченности, приведенные в предшествующей части исследования.

В качестве условий сильного шторма принимались параметры открытого моря для западного волнения со средней высотой 1.0 м и периодом 4.2 с. Соответствующие расчетные высоты  и углы подхода  на входе профилей, показанных на рисунок 3.4, варьируют в зависимости от положения уровня, что отражает таблица 3.3. Под  подразумевается угол между направлением волн и нормалью к берегу.

Таблица 3.3.

Входные параметры сильного западного шторма

Уровень, м	1.40		2.15		3.17
№ проф.	, м	, град.	, м	, град.	, м	, град.
38 54 61	0.70 0.71 0.72	52 47 47	0.79 0.81 0.81	55 50 50	0.79 0.82 0.82	58 52 52

Условия относительно слабого волнения моделировались в соответствии с таблицей 3.4, где T – период волн,  - продолжительность действия.

Таблица 3.4.

Входные параметры относительно слабого волнения

Волнение	Уровень, м	, м	T, с	, ч
1	0.2	0.4	3.2	48
2	0.6	0.6	3.8	12

3.3.  Полученные результаты

Деформации при различных положениях уровня моря.