РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
А. С. МОРОЗОВ
МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ
Конспект лекций
Рязань 2004
8.Если возможно, то составить математическую структуру модели или функциональную схему модели.
На этом этапе проводится подробное описание процесса функционирования объекта или его фрагмента. При этом подробно рассматриваются все элементы объекта, устанавливаются связи между ними, проводится описание входных и выходных потоков или сигналов их преобразования в ходе моделирования. Результатом описания объекта, как правило, является функциональная схема (структура объекта), где в качестве элементов фигурируют узлы модели с
описанием выполняемых функций и связи между элементами в виде информационных или материальных потоков.
Например, объектом моделирования является ВЦ. Входной
поток – студенты, которые приходят с интервалом времени 8![]() 2 мин. в ВЦ для работы на ЭВМ1 (ЭВМ
отладки программ) и ЭВМ2. Часть входного потока (25%) поступает на ЭВМ1, а
затем на ЭВМ2. Другая часть поступает непосредственно на ЭВМ2. После работы на
ЭВМ2 20% студентов возвращаются для повторной работы на ЭВМ1 и ЭВМ2. На входе
ВЦ имеется очередь, максимальная длина которой 4 человека. ЭВМ1 обслуживает
студентов в течение 8
2 мин. в ВЦ для работы на ЭВМ1 (ЭВМ
отладки программ) и ЭВМ2. Часть входного потока (25%) поступает на ЭВМ1, а
затем на ЭВМ2. Другая часть поступает непосредственно на ЭВМ2. После работы на
ЭВМ2 20% студентов возвращаются для повторной работы на ЭВМ1 и ЭВМ2. На входе
ВЦ имеется очередь, максимальная длина которой 4 человека. ЭВМ1 обслуживает
студентов в течение 8![]() 1 мин., ЭВМ1 – в среднем
8,5 мин.
1 мин., ЭВМ1 – в среднем
8,5 мин.
Структура объекта имеет вид рис. 1.
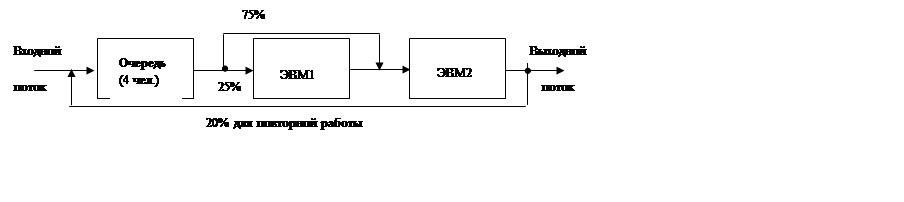 |
Рис. 1
1. 2. Описание и формализация задачи и цели моделирования
Например, в системах обслуживания задачей является
математическое описание процесса распределения ресурсов среди потока
пользователей, целью – определение таких характеристик, как коэффициент
загрузки системы Кз, средняя длина очереди на обслуживание ![]() , среднее время обслуживания одного пользователя и
, среднее время обслуживания одного пользователя и ![]() 0 т. д.
0 т. д.![]()
На этом этапе определяются состав функций, описывающих задачи и цели. Функции разделяются на детерминированные, стохастические, игровые. Для этих функций определяется область значения, описывается их характер. Если это случайная функция, то задаётся закон распределения и основные числовые характеристики. После определения состава функций проводится их аппроксимация (упрощение). Аппроксимация ведётся таким образом, чтобы упростить реализацию этих функций и получить достаточно точные характеристики, указанные в задаче и цели моделирования.
Допустим в качестве объекта фигурирует система
обслуживания, основными элементами которой являются входной поток,
обслуживающий аппарат правило обслуживания. В этом случае основными функциями,
с помощью которых можно реализовать задачу, являются функции, описывающие
процесс функционирования и формализующие указанные выше элементы. Так, по теории
массового обслуживания входной поток можно формализовать в виде ti = ti-1 + ![]() i, где ti – момент поступления в систему i-го
пользователя,
i, где ti – момент поступления в систему i-го
пользователя, ![]() i
– интервал времени между пользователями. Обслуживающий аппарат можно в виде обслуженного
входного потока t
i
– интервал времени между пользователями. Обслуживающий аппарат можно в виде обслуженного
входного потока t![]() = t
= t![]() +
+ ![]() , где t
, где t![]() -
момент освобождения аппарата от обслуживания, t
-
момент освобождения аппарата от обслуживания, t![]() -
момент начала обслуживания,
-
момент начала обслуживания, ![]() - время обслуживания
i-го пользователя. Правила обслуживания моделируются с
помощью различных условий и тестов. Например, по условию ti> t
- время обслуживания
i-го пользователя. Правила обслуживания моделируются с
помощью различных условий и тестов. Например, по условию ti> t![]() проверяется занята или свободна система, или выбор по вероятности p
проверяется занята или свободна система, или выбор по вероятности p![]() a, где 0
a, где 0![]() a
a![]() 1,
пользователь может направляться в ту или иную сторону и т. д.
1,
пользователь может направляться в ту или иную сторону и т. д.
Как правило выше рассмотренные функции случайные и
подчиняются или равномерному закону распределения в диапазоне от a до b,
или показательному закону с интенсивностью ![]() ,
и легко реализуются средствами имитационного моделирования.
,
и легко реализуются средствами имитационного моделирования.
В примере с ВЦ задачей моделирования является воспроизведение процесса обслуживания студентов вычислительным центром. В качестве цели можно взять загрузку ЭВМ1. Тогда основные функции запишутся в виде:
1. Входной поток ti = ti-1 + ![]() i, где
i, где ![]() i –
интервал поступления студентов в ВЦ.
i –
интервал поступления студентов в ВЦ.
2. Обслуживающие аппараты:
а) ЭВМ1 – t![]() = t
= t![]() +
+ ![]() ,
,
б) ЭВМ2 – t![]() = t
= t![]() +
+ ![]() ,
,
где ![]() ,
, ![]() - время обслуживания,
соответственно, ЭВМ1 и ЭВМ2; t
- время обслуживания,
соответственно, ЭВМ1 и ЭВМ2; t![]() = ti – если свободные соответствующие ЭВМ, t
= ti – если свободные соответствующие ЭВМ, t![]() = t
= t![]() , если
i-ая ЭВМ занята, t
, если
i-ая ЭВМ занята, t![]() = t
= t![]() ,
если к ЭВМ2 обращаются после ЭВМ1.
,
если к ЭВМ2 обращаются после ЭВМ1.
3. Правило обслуживания:
а) отказ из-за переполнения очереди можно выполнить по
условию ri ![]() 4, где ri
- текущая длина очереди,
4, где ri
- текущая длина очереди,
б) если допустить, что 1/4 студентов обращается к ЭВМ1
остальные к ЭВМ2, тогда по вероятности Р ![]() 0,25
можно выполнить распределение студентов,
0,25
можно выполнить распределение студентов,
в) повторная работа определяется по вероятности Р![]() 0,2.
0,2.
1. 3. Выбор и математическая запись критерия
эффективности
Под критерием понимается математическая запись оценки качества выполнения поставленной цели. Критерием эффективности может быть характеристика объекта или критерия эффективности работы объекта. После того как критерий выбран, на основе ранее выбранных теории проводится его математическая запись. При выборе математической записи критерия стремятся к тому, чтобы он был единственным, а если их множество, то независимыми друг от друга.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.