Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 14

               0 – иначе (ни то, ни другое).

например:p_i ,   i = 1, 2, 3, 4.

                      t_j ,    j = 1, 2, 3, 4.

                                                     Матрица R

	P1	P2	P3	P4
t1	1	0	1	-1
t2	-1	1	0	1
t3	0	-1	-1	1
t4	1	1	-1	0

Матрица инцидентности R разбивается на 2 матрицы: на выходную R⁺ (матрица выходных позиций) и входную матрицу R^- (матрица входных позиций).

Элементами таких матриц является:

для выходных:      1 для всех выходных позиций jго перехода, 

                                       0 – иначе.

                                      

для входных:       1 для всех выходных позиций jго перехода, 

                                     0 – иначе.

              Матрица   R⁺ (используется редко)

	P1	P2	P3	P4
t1	1	0	1	0
t2	0	1	0	1
t3	0	0	0	1
t4	1	1	0	0

                  Матрица R^- (используется часто)

	P1	P2	P3	P4
t1	0	0	0	1
t2	1	0	0	0
t3	0	1	1	0
t4	0	0	1	0

Вектор маркировки

Вектор маркировки определяет степень выполнения условий в позициях р_i. Представляет собой вектор длиной, равной числу позиций системы, и обозначается М_к(р_i). Элементами вектора является число N, определяющее степень выполнения условия позиции: N = {0, 1, 2,…}. В дальнейшем - простейшие сети Петри, в которых N = {0, 1}:  0 – условия не выполнены; 1 – условия выполнены.

Пример: вектор М₀для системы с 10-ю позициями (i = 1,…, 10) может иметь вид:   М₀ = (0 0 0 1 0 1 1 0 0 1), где порядковый номер элемента вектора соответствует порядковому номеру позиции: в позициях 1, 2, 3, 5, 8 и 9 условия не выполнены.

Правило маркировки

В процессе функционирования модели изменяется вектор маркировки, при этом таблицы остаются неизменными. При срабатывании переходов входные и выходные позиции сработанного перехода меняют своё состояние на обратное.

Если одновременно срабатывают два и более переходов, это говорит, о том, что в системе наступили параллельные процессы и их моделирование необходимо выполнять в следующей последовательности:

1)  из всех сработанных переходов по условию, установленному проектировщиком, выбирается нужный переход и с этим переходом проводятся дальнейшие изменения вектора маркировки;

2)  затем возвращаются назад и проводят работу с другим переходом и т.д., пока не будут рассмотрены все переходы.

Для того, чтобы j-ый переход сработал, необходимо, чтобы все его входные позиции (условия) были выполнены. Математически это проверяется по следующему условию: j-ый переход сработает, если вектор маркировки М_к  окажется больше или равен строке соответствующего перехода матрицы R^-: М_к, где - j-ая строка матрицы R^-. При срабатывании переходов М_к изменяет своё значение. Новое значение определяется по формуле:

, где  - j-ая строка матрицы R, (строка сработавшего перехода).

Основные характеристики сети Петри

1. Активность переходов, под которой понимается число возможных срабатываний переходов за один цикл работы модели.

Активность бывает следующих видов:

·  нулевая активность – переход за цикл не срабатывает. Это значит, что переход – тупиковый и должен быть устранён;

·  первый уровень – переход срабатывает за цикл один раз;

·  второй уровень – переход срабатывает больше одного раза.

2. Сохранность.

Часто в объекте идёт распределение ресурсов (срабатывание переходов можно принять за такт распределения ресурсов). В таких системах прверить сохранился ли объём ресурсов за цикл работы объекта или нет можно по формуле

.

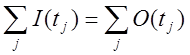3. Достижимость.

Под достижимостью понимается возможность перехода из любого j-го состояния в к-ое состояние, допустим М₀  М_кМ(С). С помощью этой характеристики определяются тупиковые позиции р_i.

Пример моделирования структуры производственного

модуля сетью Петри

 Допустим, имеется станок для обработки заготовок с магазином инструментов 1. Заготовки в таре из пункта комплектования заготовок 5 поступают в накопитель 4, из накопителя с помощью промышленного робота 3 переносятся к станку и закрепляются. Далее промышленный робот устанавливает режущий инструмент и направляется к накопителю 4.  Затем тара с помощью промышленного робота подаётся в зону выхода деталей 2. Готовая деталь транспортным механизмом 6 помещается в тару и перевозится в накопитель готовых деталей 7. Далее в накопителе 7 транспортный механизм разгружает деталь. Освободившуюся тару транспортный механизм переносит на место комплектации 5, а затем забирает очередную заготовку и доставляет её в накопитель 4.

Структура участка имеет вид:

Моделирование структуры средствами сети Петри ведётся в следующей последовательности:

1. В соответствии с описанием процесса функционирования производственного модуля определяются действия (переходы), выполняемые производственным модулем. Выделим следующие переходы:

t₁ – промышленный робот берёт старую заготовку из накопителя 4, переносит её к станку, затем закрепляет деталь и инструмент на станок.

t₂ – промышленный робот возвращается к накопителю 4, берёт пустую тару, переносит к 2 и возвращается к 4.

t₃ – станок обрабатывает деталь.

t₄ – транспортный механизм снимает готовую деталь, устанавливает её в тару, перемещает к накопителю 7 и разгружает тару.

t₅ – транспортный механизм берёт свободную тару, перевозит её в 5, загружает и перевозит в 5.