Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 2

Так, в системах обслуживания в качестве критерия можно выбрать:

К_з = / Т,                  = 1/n,             = 1/n,

где   - суммарное время обслуживания n поступивших за время проведения эксперимента (моделирования) Т пользователей; r_i – длина очереди, - время обслуживания i-го пользователя.

В рассматриваемом примере выберем К_{З ЭВМ1} = / Т.

1. 4. Определение границ модели и характера переменных

     На этом этапе в соответствии с поставленными задачей и целью из всего объекта выделяется фрагмент, подлежащий моделированию, остальная часть объекта представляется в виде внешней среды, которая  связана с моделью.

При описании внешней среды указываются только те связи, которые влияют на поставленные задачи и цели моделирования. Оставшиеся связи в модели не учитываются. Обычно связь модели с внешней средой представляется в виде входных потоков (материальных, информационных) или входных сигналов. Установленные связи подлежат математическому описанию на основе ранее выбранных теорий. Как правило, входные потоки или сигналы представляются через переменные, которые фигурируют в математической записи функции модели и критерия эффективности. При описании входных потоков и сигналов записывается их математическое выражение и, если это случайные величины, то законы распределения. Далее в математических записях функции и критерия эффективности переменные разделяются на два вида. Переменные, определяющие внешнюю среду, устанавливаются как независимые, неизменяемые переменные (наблюдаемые переменные), например  входного потока. Переменные, описывающие процесс функционирования объекта в модели представляются в виде управляемых, изменяемых переменных, то есть переменных, которые в процессе моделирования можно подбирать, изменять с целью получения  требуемых характеристик, например,  - время обслуживания. Распределённые таким образом переменные подлежат описанию. Если переменные детерминированные, то предоставляется область значения и единицы измерения, если переменные случайные, то записывается закон распределения и числовые характеристики. В итоге строится структура модели с расшифровкой всех внутренних и внешних связей между элементами. В примере фрагмент объекта, подлежащий моделированию, показан на рис. 2.

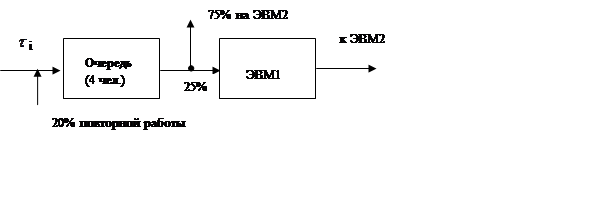                                                    Рис. 2

В модели  - управляемая переменная случайная, подчиняющаяся  равномерному закону в диапазоне от 6 до 10 мин. Переменная _i – неуправляемая случайная  с равномерным законом распределения в диапазоне от 7 до 9 мин. 

1. 5. Выбор математического аппарата и задание исходной

информации

После того как в общем виде составлены математические записи основных функций модели и внешней среды, а также критерия эффективности, переходят к выбору конкретного математического аппарата, с помощью которого наиболее просто и достаточно точно можно реализовать поставленные задачи и цели. Как правило, математический аппарат выбирается из ранее описанной теории. Для окончательной записи необходимо задать исходные данные. Такая исходная информация берется из описания процесса функционирования объекта и, если этой информации недостаточно, то проводятся дополнительные исследования или выдвигаются гипотезы, которые проверяются на аналогичных объектах.

Допустим разрабатывается имитационная модель системы обслуживания. Тогда функции модели и критерии эффективности можно реализовать с помощью датчиков случайных чисел, арифметических, логических операторов, установив в них конкретные переменные и их численные значения. Для оценки критериев эффективности достаточно собрать статистические данные по,r_i,и т.д.

1. 6. Детализация (декомпозиция) модели

     Декомпозиция модели проводится в том случае, если для выполнения поставленной цели моделирования необходимы доработки модели (более детальная проработка отдельных элементов) или структура и состав модели излишне детализированы и для выполнения поставленной цели модель можно ее свернут. Декомпозиция проводится также в тех случаях, если требуется уточнение или упрощение критерия эффективности. Если модель и задача многокритериальные и критерии к тому же зависят друг от друга, то стремятся задачу свести к единственному обобщенному критерию остальные критерии не учитываются. Если это не удается, стремятся между критериями установить линейную зависимость. Если и это не удается, подбирают удобный численный метод, с помощью которого решается многокритериальная задача с нелинейными зависимостями.

В примере из-за того, что 20% студентов обращаются в ВЦ повторно, а к ЭВМ1 – только 25%модель можно свести к виду рис. 3.

                = (81)/1,2 (мин)             = 82

                                                 Рис. 3

1. 7. Верификация модели

 Верификация-это проверка модели на степень соответствия представления объекта, выраженного в модели, реальному объекту. Верификация модели проводится несколькими способами:

     1.Верификация путем тестирования модели. В этом случае для модели задаются исходные данные такими, как предполагаемые задание исходных данных для объекта, проводятся расчеты, полученные результаты, анализируют на соответствие результатам, полученным с объекта. Если объекта не существует, то на соответствие возможным значениям, полученным на предполагаемом объекте.

     2. Верификацию проводят с помощью специальных программных средств (процессов), позволяющих проверить работоспособность модели.

1. 8.  Составление структуры модели

  Если возможно (допускает выбранный математический аппарат), то составляется математическая структура модели в виде функциональной схемы с передаточными функциями или в виде всевозможных графов.

2.  Разработка математической модели