Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 25

1.  Ввести  обозначения каждого из уравнений:

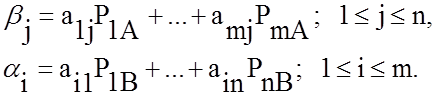
2.  Обозначить , а систему уравнений записать в виде:

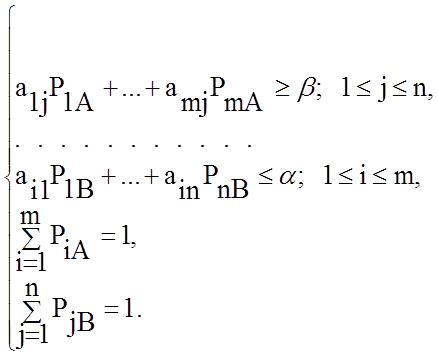
3.  Если  или  отрицательны, то путем прибавления к  постоянного числа C их приводят к положительному значению. В результате элементы матрицы примут вид:

.

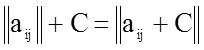4.  Перейти  к переменным 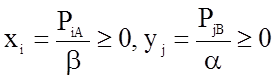, тогда система уравнений примет вид:

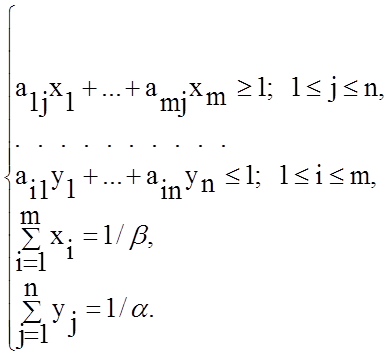
Данная система представляет собой модель двух линейных оптимизационных задач для стороны A и стороны B. Сторона A стремится найти такую стратегию, которая давала бы максимум  или минимум . В то же время сторона B ищет такую стратегию, которая давала бы минимум

 или максимум .

Следовательно, в качестве целевой функции для стороны A можно записать: ,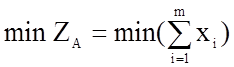

а систему ограничений представить в виде:

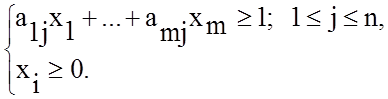
Для стороны B запишем целевую функцию 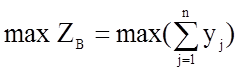 и систему ограничений:

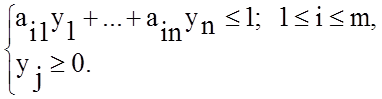
Определяя из первой задачи , из второй задачи , найдем  следующим образом:

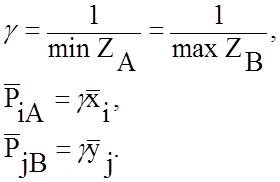
Если при решении задачи вводилось смещение величиной C, то при определении среднего выигрыша  необходимо выполнить действие .

Кооперативные игры

В конфликтных ситуациях участники могут объединяться в коалиции и выступать группами друг против друга. Такие игры называются кооперативными и в них  помимо ранее изложенных проблем (поиск оптимальных стратегий) встает необходимость правильного дележа выигрыша между участниками коалиции.

В дальнейшем рассмотрим игры, в которых определяется структура коалиций. С помощью структуры каждый из участников определяет для себя целесообразность вступления в ту или иную коалицию. Целесообразность определяется величиной выигрыша участника в результате проведенной игры.

Допустим, в игре участвует множество {N} участников. Из этого множества могут быть сформированы коалиции (группы) числом участников . Число возможных коалиций определяется по формуле .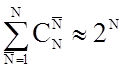

При правильно выбранной стратегии  коалиция сможет получить максимальный выигрыш , который называется характеристической функцией.

Считается, что если имеются коалиции , то сумма выигрыша всех коалиций должна быть меньше или равна выигрышу коалиции объемом N (когда все участники в одной группе), т.е. .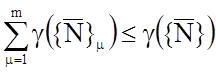

В результате деления выигрыша каждому участнику коалиции достанется выигрыш . Игра и коалиции составлены правильно, если выигрыш участника коалиции  окажется больше или равен выигрышу участника, выступающего самостоятельно:

Распределение выигрыша между участниками математически задается в виде вектора дележа .

При составлении вектора дележа учитываются два условия:

Основной целью кооперативной игры является поиск оптимального (справедливого) вектора дележа. Поиск осуществляется методом сравнения векторов дележей. Вектор дележа называется доминирующим (лучшим), если его  больше, чем  другого вектора.

Пусть имеем два вектора дележа:

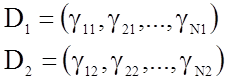
Считается, что если , то вектор  доминирует над вектором .

 Оптимальный вектор называется ядром игры . Дележ с помощью ядра игры называется равноценным делением (оптимальный дележ).

Методика поиска оптимального дележа

1.  Составляется дележ . В дальнейшем значения  по договоренности не изменяются.

2.  Всех присоединяющихся участников коалиции делят на полезных () и бесполезных ().

3.  Выигрыш каждого участника определяется суммой выигрышей, полученных  при участии в различных коалициях, т.е. .

4.  Составляется вектор Шепли (ядро Шепли). В ядро Шепли включают полезных участников. Для этого проверяют, приносит ли дополнительный выигрыш для коалиции новый участник, по условию .

5.  Если участник полезный, то выигрыш каждого участника  в векторе дележа определяется по формуле ,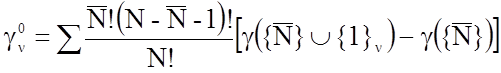

где -члены вектора Шепли (),  -возможные коалиции без участника ,  -коалиции с участником .

Пример кооперативной игры

Пусть трем автомобилестроительным комбинатам необходим завод по выпуску шин. Строить завод можно на паях или отдельно каждому комбинату, например, по цеху. В этом случае возможны следующие коалиции участников:

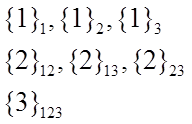-  каждый комбинат в отдельности,

-  два комбината,

-  три комбината.

Расходы на строительство, затрачиваемые коалициями, сведены в таблицу:

Коалиции
Стоимость работ	200	300	250	400	390	500	600

Рассчитаем сумму взносов на строительство каждого из участников в различных коалициях:

1.  Коалиция . Тогда остальные возможные коалиции .

Определим сумму взносов 1-го участника по формуле Шепли

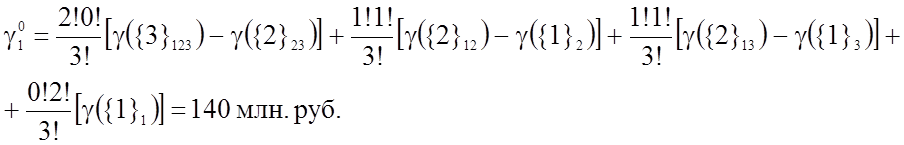
По аналогичной формуле можно определить сумму взносов 2-го и 3-го участников:

Общая сумма взносов:   

2.  Коалиции . По формуле Шепли определяется сумма взносов участников в коалиции в млн. руб.

Для коалиции :  ,

для коалиции :  ,

для коалиции :  .

3.  Из сравнения полученных дележей (сумм взносов на строительство) следует, что наилучшая коалиция , имеющая дележ

. При этом каждый из участников, вступая в такую коалицию, по сравнению с индивидуальным строительством будет иметь соответственно выигрыш 60 млн. руб., 55 млн. руб., 45 млн. руб.

Литература

1.  Гультяев А.К. MatLab 5.2. Имитационное моделирование в среде Windows. Практическое пособие. – С.Пб.: Крона принт, 1999.

2.  Советов Б.Я., Яковлев С.А. Моделирование систем. М.: Высш. шк.,   2001.

3.  Маклаков С.В.  BpWin  и ErWin CASE – средства разработки информационных систем. М.: Диалог – МИФИ, 2001.

4.  Калянов Г.Н. Консалтинг при автоматизации предприятий: подходы, методы, средства. М.: Синтег, 1997.

5.  Морозов А.С. Математические основы анализа и синтеза систем/ Метод. указ. к лаб. работам. Рязань, РГРТА, 2000, 3079. 

6.  Морозов А.С. Вычислительные модели автоматизированных производств/ Метод. указ. к лаб. работам. Рязань, РГРТА, 1997, 2627.