Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 20

Например, в рассмотренных выше сущностях СОТРУДНИК и ИСТОРИЯ_З/ПЛ_КАРЬЕРЫ можно установить следующие связи. Сущность СОТРУДНИК с сущностью ИСТОРИЯ_З/ПЛ_КАРЬЕРЫ связана одинарным отношением. В то же время сущность ИСТОРИЯ_З/ПЛ_КАРЬЕРЫ связана с сущностью СОТРУДНИК многократным отношением, т.к. атрибуты должность, з/пл, дата_изменения могут принимать различные значения (0,1,…,n) для данного сотрудника. Тогда структура связей примет вид:

 

3. Разрешение неспецифических отношений (n:m)

Если в отношениях существуют связи n:m, их необходимо свести, по крайней мере, к двум специфическим отношениям (1:n).

Например, между сущностями СТУДЕНТ и ПРЕДМЕТЫ неспецифическое отношение (n:m), т.к. множество студентов изучают множество предметов.

 

ИЗУЧЕНИЕ_ПРЕДМЕТА

ПРЕДМЕТЫ

СТУДЕНТ

Путем введения дополнительной сущности ИЗУЧЕНИЕ_ПРЕДМЕТА отношение можно свести к специфическим отношениям (1:n), т.е. один студент изучает конкретные предметы, которых множество.

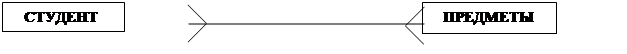2. 8. 10. Составление спецификации управления (STD)

STD представляет собой модель реакции системы на события, происходящие в ней. Для составления спецификации пользуются следующей терминологией:

- СОСТОЯНИЕ определяет условия устойчивости системы; имя состояния определяется названием состояния, в котором находится система (например, нагревание, охлаждение);

- ПЕРЕХОДопределяет переход системы из одного состояния в другое; имя перехода определяется событием, которое является причиной перехода, или именем управляющего потока (например, пароль введен);

- УСЛОВИЕопределяет события, вызывающие переход; как правило, оно носит имя этого события или имя управляющего потока (например, “пароль”=007);

- ДЕЙСТВИЕ-это операция перехода; носит название действия, вызванного управляющим потоком (например, “введенная карта”=истина).

Графически спецификация представляется в следующем виде:

 

                                                                                                           УСЛОВИЕ

                                                                                                        

                                                                                                           ДЕЙСТВИЕ

	СОСТОЯНИЕ 2

 

Пример составления спецификации управления для банковской задачи

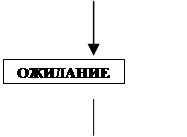
В задаче рассматриваются два состояния: ожидание и обработка; условие: введенная кредитная карта; действие: получить пароль.

 

                                                      ВВЕДЕННАЯ КРЕДИТНАЯ КАРТА

 

                                                                  ПОЛУЧИТЬ ПАРОЛЬ

 

3.  9. Модели синтеза систем управления

Совершенствование, повышение эффективности организации, планирования и управления требует построения и проведения работы системы (объекта, процесса) таким образом, чтобы функционирование обеспечило максимальный эффект. 

Так в задачах синтеза систем необходимо из области допустимых значений  выбрать такие значения параметров , которые приводили бы к наиболее эффективному синтезу объекта. Эффективность синтеза оценивается критерием эффективности или целевой функцией .

С математической точки зрения моделью оптимизационной задачи синтеза является запись целевой функции , установление множества параметров , а также определение области значений (ограничений) параметров .

 Как правило, число неизвестных параметров больше числа ограничений, накладываемых на значения параметра, т.е. некоторые из параметров (обычно не известно какие) не имеют ограничений. Целью моделирования является выбор значений множества X, при которых целевая функция y достигает своего экстремального значения.

Модели бывают следующих видов:

1.  Линейная модель. В линейной модели , где , находятся в линейной зависимости      друг от друга. Область определения или ограничения записываются в виде системы линейных алгебраических уравнений:

.

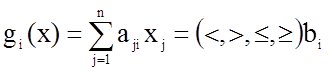Целевая функция линейна и записывается в виде:

.

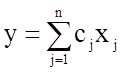          В линейной задаче коэффициенты  известны.

2.  Нелинейная модель. Среди нелинейных моделей наиболее изучены модели, в которых ограничения  линейны, а все остальное может быть нелинейным. При этом целевая функция должна быть записана в виде суммы отдельных функций по одному параметру:

.

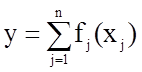Рассмотренные модели используются в следующих видах задач:

1)  распределительные задачи, в которых множество ограниченных    ресурсов  необходимо распределить между множеством пользователей  таким образом, чтобы использование ресурсов было наиболее эффективным;

2)  задача управления запасами, в которой запасы, требующие для своей доставки и хранения определенных затрат, необходимо создавать таким образом, чтобы их использование было наиболее эффективным;

3)  задача замены оборудования, целью которой является разработка порядка эксплуатации, ремонта и замены оборудования, при котором достигается наибольшая эффективность производства.

Методы решения оптимизационных задач

Для решения оптимизационных задач широко используются два метода:

1)  линейное программирование,

2)  динамическое программирование.

Под программированием понимается планирование решения задачи, т.е. составление последовательности выполнения вычислительных процедур, приводящих к оптимальному решению задачи.

Линейное программирование