Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 23

                                                                         

 

                                                                                                  

                                                                       

                                                                         

                                                                                                                                                                                  

                                                                         

                                                                         

 

                                                                                                        

                                                                                                  

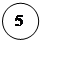
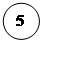
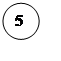
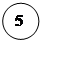
Решение задачи

1.  Для поиска условного оптимума запишем уравнение Беллмана на k-ом и n-ом шагах:

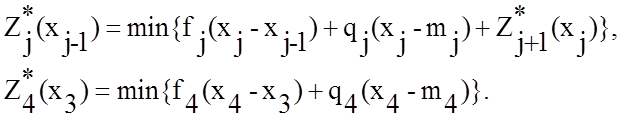
2.  Определим условные оптимумы.

1) Определим условный оптимум на 4-ом шаге , при этом варьируя переменными x₃ и x₄. Составим таблицу:

x3	x4	Z4	Параметры, определяющие min Z4			Uk
			x3	x4
1	0  1	18  0	1	1	0	0
2	0  1  2	25  7  8	2	1	7	-1
3	0  1  2	32 14 15	3	1	14	-2

Из таблицы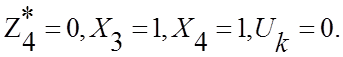

2)  Определим условный оптимум на 3-ем шаге , при этом принимая за оптимальное значение x₄=1 и варьируя x₂ и x₃. Составим таблицу:

x2	x3	Z3	Параметры, определяющие min Z3			Uk
			x2	x3
2	0  1  2  3	57 29 18 24	2	2	18	0
3	0  1  2  3	64 36 25 14	3	3	14	0
4	2  3  4	32 21 29	4	3	21	-1

Из таблицы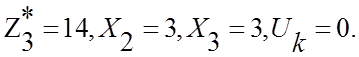

3)  Определим условный оптимум на 2-ом шаге , принимая x₄=1, x₃=3 и варьируя x₁ и x₂. Составим таблицу:

x3	x4	Z2	Параметры, определяющие min Z2			Uk
			x3	x4
2	2  3  4	51 46 52	2	3	46	+1
3	2  3  4	56 36 42	3	3	36	0
4	2  3  4	65 43 32	4	4	32	0

Из таблицы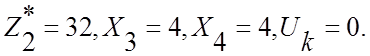     

4)  Определим условный оптимум на 1-ом шаге . Здесь x₀=2, варьируем x₁. Составим таблицу:

x0	x1		Uk
2	2	46	0
2	3	54	+1

Из таблицы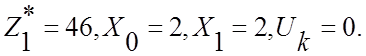

3.  Построим ряд условных оптимумов: .

Построим ряд безусловных оптимумов:

Таким образом, для оптимального управления производством необходимо 1-ый месяц использовать нормативное число работников, на 2-ом месяце - число работников увеличить на 1, на 3-ем месяце - число работников

сохранить, на 4-ом месяце - 2-х работников уволить.

2.10. Игровые модели

При проектировании и эксплуатации систем возникают конфликтные ситуации, когда сталкиваются противоположные интересы. Каждая из сторон участниц конфликта стремится решить свою проблему за счет другой стороны и принимает против другой стороны определенные стратегии поведения. Для разрешения таких ситуаций используется математический аппарат, называемый теорией игр.

Допустим, в конфликте участвует множество сторон {U}. Каждая из сторон, допустим C, имеет в рассматриваемой игре набор стратегий . В результате разрешения конфликта получается множество исходов конфликтной ситуации .

Для математической записи конфликтной ситуации вводится функция проигрыша-выигрыша участников конфликта. Математически проигрыш-выигрыш при применении каждой из сторон своей стратегии представляется в виде платежа , определяющего величину проигрыша-выигрыша (платежа) за выход из конфликтной ситуации при условии, что одна из сторон применила стратегию , а другая - стратегию .

Различают следующие виды игр:

1)  коалиционная игра, когда в игре участвует множество сторон, причем в каждой стороне несколько участников;

2)  бескоалиционная игра, когда в игре два участника.

Вышеуказанные игры подразделяются на следующие:

-  бескомпромиссные игры, когда проигрыш одной из сторон является выигрышем другой стороны;

-  компромиссные игры, когда о размере проигрыша-выигрыша возможны договоренности.

В дальнейшем рассматриваем бескоалиционные бескомпромиссные игры.

В качестве модели игры используется платежная или нормальная матрица игры. Матрица представляет собой платежи  за выход из конфликтной ситуации. Строками матрицы являются стратегии стороны A, столбцами - стратегии стороны B. В общем случае матрица может быть представлена в виде