Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 6

     Пример последовательной проводки. Допустим, имеется система обслуживания, в которую поступают требования на обслуживание в случайном порядке. Система состоит из одного обслуживающего аппарата и ограниченной очереди. Дисциплина обслуживания- в порядке очереди. В этом случае принцип последовательной проводки реализуется следующим образом. Требование загоняется в систему (алгоритм), затем проверяется состояние системы (занята, свободна). Если свободна, то требованию приписывается время обслуживания, затем оно поступает в блок сбора и обработки информации и далее передается на блок формирования момента поступления нового требования. Если на момент прихода требований система занята, то оно направляется в блоки, реализующие очередь. В этих блоках требованию приписывается характеристика нахождения в очереди, затем оно передается в блок обслуживания. Там ему приписывается характеристика обслуживания и передается в блок сбора и обработки информации, а затем на вход, формирующий поступление требований в систему.

2. 2. 2. Методика построения имитационной модели

     Имитационная модель строится в четыре этапа:

1. Выбор и составление имитаторов основных функций объекта и внешней среды (имитаторов, реализующих задачу  моделирования);

2. Составление имитаторов сервисных функций, к которым относятся установка

исходных данных, сбор и обработка статистических данных, организация эксперимента;

3. Составление структуры моделирующего алгоритма;

4. Описание алгоритма.

Выбор имитаторов основных функций

    Допустим в качестве объекта моделирования выбираем систему обслуживания, для которой основными функциями являются обслуживание  пользователей по определенным правилам. Система включает в себя три элемента, функционирование которых необходимо имитировать.

     1.Входные потоки. Для этих потоков согласно концептуальному моделированию необходимо выбрать датчик случайных чисел t_i  с заданным законом распределения f(t), а также необходим вычислитель                                                              

ДСЧ

                                         t_i+1=t_i+t_i .                             t_i                           t_i+1

 2. Для имитации процесса обслуживания необходим датчик случайных чисел

(ДСЧ), определяющий время обслуживания t_I^o. Помимо ДСЧ  необходим вычислитель (арифметический оператор), определяющий момент окончания обслуживания i-го пользователя

                                       t_i^осв=t_i^н+t_i^o.

ДСЧ

                                                                     t_i                                                                                                               t^o

Датчик времени обслуживания имеет закон распределения времени обслуживания Ф(t^о).

     Если в системе имеются очереди, для их имитации необходимы 1)счетчики числа поступления в очередь типа k=k+1; 2)ДСЧ, определяющие max допустимое время нахождения пользователя в очереди t_I^oж; 3)вычислитель момента окончания ожидания t_i^ож=t_I^ож+t_i. Датчик максимально допустимого времени ожидания подчиняется закону распределения h(t^ож).

3. Имитация правил обслуживания. В системах обслуживания помимо ранее указанных правил существуют общие правила, по которым происходит передача данных от одного оператора к другому, а также правила присвоения значений переменным.

     В имитационной модели эксперимент считается законченным, если момент поступления пользователя в систему превышает время моделирования Т. Для реализации этого правила в алгоритме предусматривается оператор сравнения t_i³Т. Определение состояния системы (занято, свободно) в алгоритме осуществляется по условию t_i<t_i-1^осв. В системах с ограниченной очередью условие того дождется ли пользователь обслуживания определяется по условию t_i^ож£t_i-1^осв. В системах с очередью необходимо знать момент начала обслуживания t_i^н. Эта переменная  определяется двумя операторами присвоения. Если пользователь обратился к свободной системе, то t_i^н=t_i, если к занятой, то t_i^н=t_i-1^осв.

Составление имитаторов «сервисных» функций

     Установка исходных данных. Для того чтобы каждая серия экспериментов проводилась при одинаковых и  соответствующих объекту данных, в алгоритме необходимо предусмотреть блоки присвоения начальных значений переменным, например:

              t_i=0         ;          t_i^осв=0         ;            t_i=0           ;              t_i^ож=0.

      Сбор и обработка статистических данных. В системах обслуживания, как

правило, необходимо определить случайную величину ( математическое ожидание), поэтому для ее поиска  используется арифметические устройства статистической обработки данных в виде определителя математического ожидания случайной величины

                                 ,

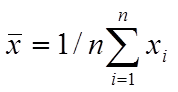где x_i-значение случайной величины, полученное в i-том эксперименте;

      n-число проведенных экспериментов.

Помимо математического ожидания, определяется дисперсия случайной величины. Для этого необходим вычислитель дисперсии

                                             .

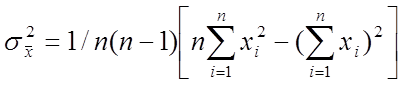Следовательно, для сбора и обработки статистических данных необходимы сумматоры x_i , сумматоры x_i²,  вычислители средних значений случайной величины и дисперсии случайной величины.

     Проведение эксперимента. Для того чтобы получить статистически устойчивые данные, необходимо провести требуемое число экспериментов. Существуют три различных подхода для определения требуемого числа эксперимента:

1. Эксперимент считается законченным, если истекло модельное время T. Модельное время Т обычно задается при выборе оценок цели моделирования в виде времени, за которое определяется характеристика.

2. Определяется предварительно (в концептуальном моделировании) требуемое число прогонов, при проведении которых погрешность результатов эксперимента не превышает заданное значение e.

3. Число экспериментов определяется автоматически. Эксперимент заканчивается, если дисперсия искомой характеристики не превышает заданное значение.