4. Составляется система дифференциальных уравнений. Число уравнений соответствует числу состояний системы. Допустим, необходимо записать уравнение для состояния si. Запись ведется в следующей последовательности с использованием мнемонического правила. В левой части уравнения записывается 1-ая производная вероятности состояния si, то есть dpi(t)/dt. В правой части уравнения записывается сумма произведений интенсивности перехода на вероятности состояния системы. При этом произведение положительно, если система входит в описываемое состояние, отрицательна, если система выходит из этого состояния.
В рассматриваемом примере запишем уравнение для состояния s4:
![]()
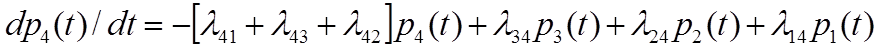 .-
.-
Для того чтобы получить ненулевые решения системы,
необходимо вместо одного из уравнений записать сумму 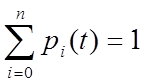 .
.
Если необходимо определить вероятности состояний системы в установившемся режиме, надо систему дифференциальных уравнений привести к системе линейных алгебраических уравнений.
Зная вероятности системы как результат решения системы дифференциальных уравнений, можно определить различные характеристики системы обслуживания.
2. 1. 4. Основные характеристики системы обслуживания
1.Вероятность отказа R определяется по формуле:
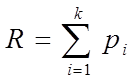 ,
,
где pi- вероятность состояния системы, при котором пользователю даётся отказ в обслуживании.
2.Вероятность обслуживания: Q=1-R
3.Среднее время обслуживания одного пользователя:
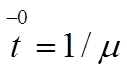 ,
,
где m- интенсивность обслуживания. Формула справедлива для простейших потоков обслуживания.
4. Средняя длина очереди на обслуживание:
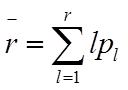 ,
,
где pl – вероятность того, что в очереди находится l пользователей.
Средняя длина очереди математически связана со
средним временем ожидания пользователя обслуживания 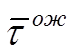 следующим
образом:
следующим
образом: 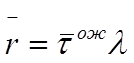 ,
,
где l - интенсивность поступления пользователей в систему .
5. Коэффициент загруженности i -го обслуживающего аппарата:
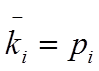 ,
,
где pi-вероятность занятого состояния обслуживающего аппарата.
2. 2. Имитационное моделирование
Имитационная модель представляет собой вычислительный алгоритм, в котором реализован принцип имитации (воспроизведения) последовательности выполнения операций, протекающих в реальном объекте. Имитационная модель имитирует процесс функционирования реального объекта средствами вычислительной техники.
Поиск характеристик объекта осуществляется путём проведения эксперимента на модели и обработки полученных данных. Имитационное моделирование используется в тех случаях, если аналитическую модель создать невозможно или же созданная модель сложна в реализации. Как правило, имитационная модель легко реализуема и имеет достаточно высокую точность.
2. 2. 1. Принципы построения моделирующего алгоритма
В имитационной модели необходимо предусмотреть так называемое наращивание времени, то есть увеличение времени от начального до конечного значения. Это необходимо для того, чтобы: 1)получить временные характеристики zi (t); 2) получить средние по времени характеристики (статические характеристики).
Для наращивания времени в модели используются два принципа:
1. принцип Dt;
2. принцип особых состояний системы.
Принцип Dt
По принципу Dt время, в течение которого определяется характеристика, наращивается дискретно, с шагом Dt. То есть к каждому последующему моменту добавляется Dt и определяется характеристика в новый момент времени. Для детерминированной системы zi (t) определяется, начиная с момента t0 и далее t1=t0+Dt, t2=t1+Dt. В результате в иском интервале получаем дискретную функцию zi (t). Обычно известны начальные условия zi (t0) и интервал времени, в котором необходимо определить характеристики. Исходя из изложенного в алгоритме необходимо предусмотреть блок наращивания времени.
Для того чтобы определить случайную временную функцию в стохастических системах по принцип Dt в алгоритме необходимо предусмотреть: 1)блок наращивания времени; 2)имитаторы значений функции в различные моменты времени. Определение функции в этом случае ведется следующим образом. В момент t0 из ряда распределения вероятностей значения функции выбирается одно из значений. Выбранное значение принимается за начальное, далее наращивается время. С новым моментом времени проводится серия испытаний. В результате этих испытаний создается ряд, далее из ряда случайным образом выбирается одно из значений, наращивается время и проводится новая серия испытаний и так далее, пока не истечет время.
Таким образом строится одна из множеств реализаций искомой характеристики.
Для того чтобы получить статистически устойчивую характеристику, рассматривают множество реализаций.
Принцип Dt используется только в системах, допускающих достаточно большой шаг Dt, так как требует для своей реализации большое машинное время, особенно для стохастических систем. Для устранения указанного недостатка используют принцип особых состояний.
Принцип особых состояний
Система во время функционирования может находится в двух состояниях: в особом, когда ее характеристики изменяются достаточно быстро и неособом, когда ее характеристики или вовсе не изменяются, или изменяется незначительно.
В связи с этим построение временных характеристик на время нахождения системы в неособом состоянии можно исключить, и определять характеристики на момент особых состояний, тем самым существенно сократив число экспериментов. При реализации такого принципа необходимо в алгоритме предусмотреть блок, определяющий момент вхождения системы в особое состояние.
Для упрощения алгоритма, имитирующего процесс функционирования объекта, используется принцип последовательной проводки пользователей системы. Пользователь последовательно проводится по блокам алгоритма, в каждом из блоков определяется его характеристики, собираются по нем статистические данные и он выводится из системы. После этого система готова к приему следующего пользователя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.