Данную задачу можно представить в виде графа, с помощью которого можно найти оптимальный путь перехода из начального состояния в конечное.
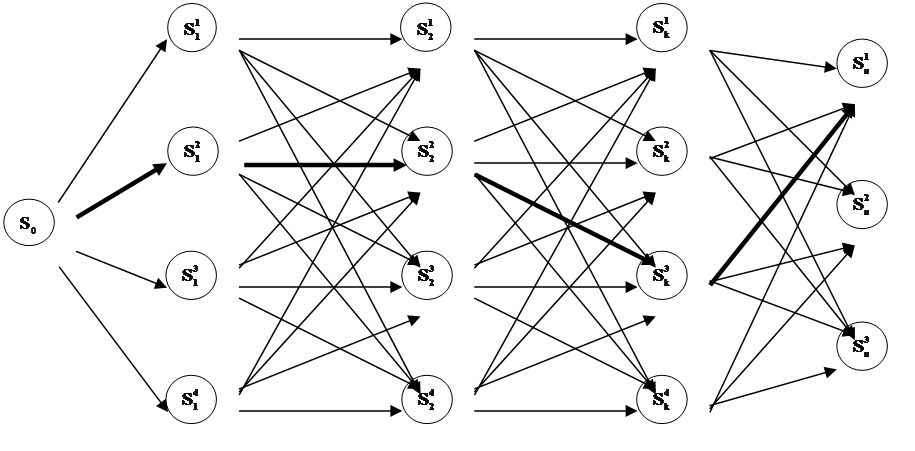 |
Такого рода задачи решаются методом динамического программирования (оптимального управления Беллмана). Для этого составляется специальная модель системы, для которой необходимо определить следующие данные:
1)
вид состояния системы ![]() и установить связь его с предыдущим
состоянием
и установить связь его с предыдущим
состоянием ![]() и управлением
и управлением ![]() , т.е. записать функцию
, т.е. записать функцию ![]() ;
;
2)
эффективность перехода из
состояния ![]() в состояние
в состояние ![]() под
воздействием управления
под
воздействием управления ![]() в виде
в виде ![]() ;
;
3)
общую целевую функцию,
определяющую эффективность перехода системы из начального состояния ![]() в конечное
в конечное ![]() под
воздействием управления
под
воздействием управления ![]() , в виде
, в виде ![]() .
.
Если общая целевая функция не аддитивна, т.е. не записана в виде
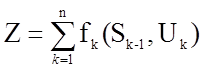 , то ее необходимо свести к
аддитивной форме. Например, если целевая функция мультипликативна, т.е.
записана в виде произведения,
, то ее необходимо свести к
аддитивной форме. Например, если целевая функция мультипликативна, т.е.
записана в виде произведения,
то путем логарифмирования ее нужно свести к аддитивной форме
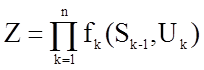
![]() .
.
Задачей динамического программирования является поиск на каждом шаге такого управления, при котором общая целевая функция принимает максимальное значение. Если в исходной задаче установлен минимум целевой функции, то, путем смены знака в целевой функции на обратный, задача сводится к поиску максимума.
Метод оптимального управления Беллмана
Суть метода оптимального управления Беллмана состоит в
том, что если система находилась в состоянии ![]() ,
то необходимо найти оптимальное управление
,
то необходимо найти оптимальное управление ![]() ,
которое на последующих шагах k+1,…,n приводило бы к максимуму целевой функции
,
которое на последующих шагах k+1,…,n приводило бы к максимуму целевой функции ![]() .
.
![]() носит название
локального оптимума на k-ом шаге.
носит название
локального оптимума на k-ом шаге.
Беллман предложил следующий путь поиска локального оптимума. Записывается уравнение целевой функции на k-ом шаге в виде:
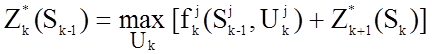 ,
,
где ![]() ,
, ![]() -оптимальная (максимальная) целевая
функция или локальный оптимум на k+1 шаге.
-оптимальная (максимальная) целевая
функция или локальный оптимум на k+1 шаге.
Из уравнения видно, что оптимальная целевая функция на k-ом шаге определяется путем поиска максимума суммы оптимальной целевой функции на (k+1)-ом шаге и эффективности перехода из (k-1)-го состояния в k-ое состояние.
Пользуясь указанной формулой, Беллман предложил оптимальную целевую функцию, а следовательно, и оптимальное управление для каждого
k-го состояния
определять, начиная с конечного состояния ![]() ,
т.е. двигаясь с конца к исходному состоянию. Такое предложение позволяет
существенно упростить расчеты, т.к.
,
т.е. двигаясь с конца к исходному состоянию. Такое предложение позволяет
существенно упростить расчеты, т.к.
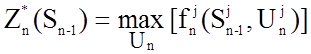 .
.
Для вычисления целевой функции на (n-1)-ом
шаге используется оптимальная целевая функция на n-ом шаге ![]() :
:
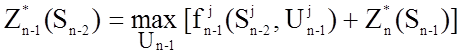 .
.
Зная оптимальную целевую функцию на (n-1)-ом шаге, можно найти оптимальную целевую функцию на (n-2)-ом шаге и т.д. до 1-го шага.
Таким образом, можно построить ряд локальных
(условных) оптимумов. Условность состоит в том, что оптимальный переход
находится при условии, что система вначале находилась в состоянии ![]() . Ряд условных оптимумов представляется
в виде последовательности
. Ряд условных оптимумов представляется
в виде последовательности ![]() .
.
Для каждого условного оптимума определяется условное
оптимальное управление в виде последовательности ![]() .
.
Окончательным решением задачи является определение
безусловных оптимумов и безусловных оптимальных управлений, т.е. необходимо
выстроить ряд вида: ![]() .
.
Методика построения модели и решения задачи средствами
динамического программирования
Построение модели ведется в следующей последовательности:
1.
В поставленной задаче выделяются
состояния ![]() и выбирается способ деления процесса
на шаги.
и выбирается способ деления процесса
на шаги.
2.
Каждое из состояний Sk представляется в виде множества подсостояний ![]() и
определяется управление
и
определяется управление ![]() .
.
3.
Записывается уравнение,
определяющее состояние ![]() и являющееся функцией
предыдущего состояния
и являющееся функцией
предыдущего состояния ![]() и управления
и управления ![]() , в виде
, в виде ![]() .
.
4.
Вводится показатель эффективности
для каждого k-го перехода: ![]() .
.
5.
Составляется общая целевая функция
в виде суммы эффективностей на k-ых шагах: 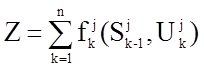 .
.
6. Строится граф модели.
Этапы решения задачи следующие:
1.
Записываются уравнения Беллмана для
k-го и n-го шагов:![]()
![]()
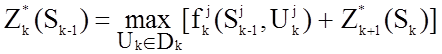 ,
,
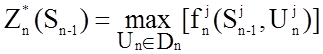 .
.
2.
Определяется условное оптимальное
управление ![]() .
.
3. Строится ряд безусловных оптимумов и безусловного оптимального управления. Если начальное состояние S0 единственное, то максимум
общей целевой функции равен условному оптимуму 1-го
перехода ![]() .
.
Далее выстраивается ряд ![]() .
.
4. Если начальных состояний несколько
и они составляют множество ![]() , то максимум
целевой функции определяется по формуле
, то максимум
целевой функции определяется по формуле 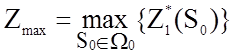 .
.
Далее строится ряд ![]() .
.
Пример решения задачи методом динамического программирования
Планируется производство на 4 месяца. Необходимое
число работников на каждый месяц известно: ![]() .
Перед началом работ
.
Перед началом работ ![]() . Допустим, что работа j-го
месяца может быть выполнена меньшим числом работников. Пусть
. Допустим, что работа j-го
месяца может быть выполнена меньшим числом работников. Пусть ![]() - фактическое число работников в j-ом
месяце, где j=1,2,3,4. Затраты на изменение численности работников
при переходе от (j-1)-го месяца к j-му
определяются по формуле
- фактическое число работников в j-ом
месяце, где j=1,2,3,4. Затраты на изменение численности работников
при переходе от (j-1)-го месяца к j-му
определяются по формуле ![]() и в зависимости
от знака определяют найм или увольнение работника. В начальный момент
и в зависимости
от знака определяют найм или увольнение работника. В начальный момент ![]() . Отклонение от числа запланированных
работников mj приводит к дополнительным расходам
. Отклонение от числа запланированных
работников mj приводит к дополнительным расходам ![]() . В начальный момент
. В начальный момент ![]() .
.
Построение модели
1. Задача разбивается по месяцам на 4 шага: j=1,2,3,4.
2.
За состояние системы на k-ом
шаге принимается число работников ![]() , управление на k-ом
шаге
, управление на k-ом
шаге ![]() .
.
3.
Устанавливается связь состояния Sk с предыдущим состоянием и с управлением ![]() .
.
4. По данным предприятия записывается эффективность перехода на каждом k-ом шаге
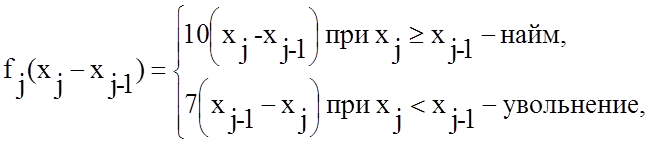
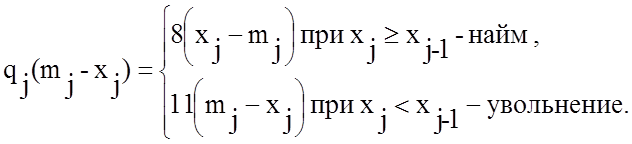
5.
Общая целевая функция имеет вид 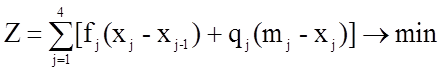 .
.
6. Строится граф задачи вида
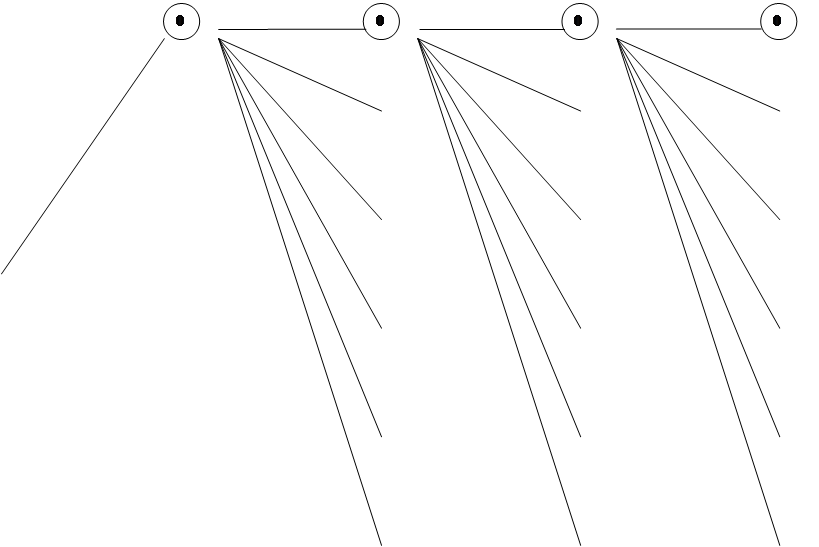 |























![]()
![]()




![]()

 |
|||||
 |
 |
||||
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.