Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 21

Линейное программирование применяется для решения линейной оптимизационной задачи, поэтому вначале составляется модель линейной оптимизационной задачи в следующей последовательности:

1)  записывается вектор X представляющий собой множество линейно зависимых переменных (параметров)

;

2) составляется целевая функция (критерий эффективности) в виде

;

3)  записывается система линейных алгебраических неравенств в виде

.

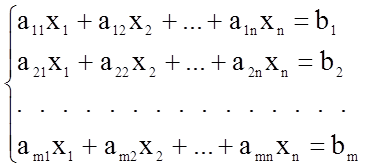
В системе  представляет собой ресурсы, - расход j-ых ресурсов на     i-ый параметр. Если в системе есть неравенства, то необходимо перейти к равенствам путем введения дополнительных переменных  Из системы видно, что число уравнений m всегда меньше числа переменных n.

Целью моделирования является поиск таких значений , при которых целевая функция  достигает своего минимума. Если первоначально целевая функция записана под поиск максимума, то необходимо  знаки ее переменных сменить на обратные, т.е. записать в виде Ф(-Х).

Пример составления модели линейной задачи

Цех выпускает валы и втулки. На производство 1 вала рабочий тратит     3 часа, а на производство 1 втулки - 2 часа. От реализации вала предприятие получает прибыль 800 руб., от реализации втулки - 600 руб. Цех должен выпустить не менее 100 валов и не менее 200 втулок. Сколько валов и втулок должен выпустить цех, чтобы получить наибольшую прибыль, если фонд рабочего времени составляет 900 человек - часов?

В качестве переменных (параметров) выбираем: - число валов,           - число втулок. Затраты на выпуск 1 вала обозначим =3 час/вал, на выпуск 1 втулки - =2 час/втулка. Прибыль от реализации 1 вала            =800 руб./вал, от реализации 1 втулки - =600 руб./втулка. Ресурсы рабочего времени =900 человек - часов. Условия по выпуску валов и втулок: , .

Таким образом, модель запишется в виде:

- множество параметров ;

- ограничения  ;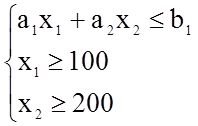

- целевая функция       .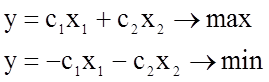    

Далее систему неравенств сведем к системе равенств: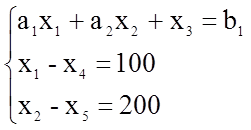

Симплекс-метод решения задач

линейного программирования

Как правило, в линейной задаче число уравнений меньше числа неизвестных. Следовательно, однозначно можно определить число неизвестных, равное числу уравнений. Остальные неизвестные определить нельзя, поэтому их при решении линейных задач принимают за свободные переменные и приравнивают их к нулю.

Решение линейной задачи симплекс-методом ведется в следующей последовательности:

1.  Из вектора переменных размерностью n выбирают переменные, число которых равное числу уравнений ограничений m, их принимают за однозначно определенные (базовые) переменные. Остальные (n-m) переменных принимают за свободные и приравнивают их к нулю.

2.  Базовые переменные, исходя из уравнений ограничений, выражают через свободные переменные в виде линейной комбинации

После преобразования оставляется каноническая форма записи модели. Эту запись иногда называют симплекс-планом или опорным планом. Модель записывается в виде следующей системы уравнений:

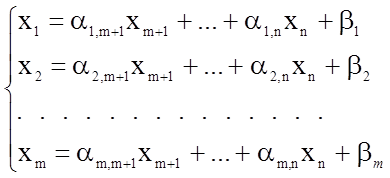
Для того чтобы проверить отвечает ли составленная система поставленной цели, необходимо полученные значения базисных переменных подставить в целевую функцию:

,

где - значение целевой функции, определяемое  и проанализировать полученную целевую функцию. Если в целевой функции все коэффициенты , то опорный план оптимальный. Следовательно,

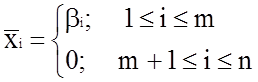
Если в целевой функции некоторые коэффициенты <0, то план не оптимален. Необходимо строить новый план. Для этого по симплекс-методу одну из свободных переменных (у которой ) необходимо перевести в разряд базисных, а одну из базисных переменных перевести в разряд свободных и составить новый опорный план. Далее процедуру повторяют. Смену переменных выполняют следующим образом.  В разряд базисных переводят ту свободную переменную, у которой больше абсолютное значение коэффициента. Затем в выше рассмотренном опорном плане проверяется, какая из базисных переменных при увеличении выбранной свободной переменной быстрее устремляется к нулю. Эту переменную переводят в разряд свободных.

Пример решения задачи симплекс-методом

Для задачи, рассмотренной выше, запишем  модель в виде:

-  целевая функция (критерий эффективности)

;

-  ограничения (область определения)

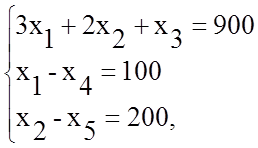
где - неиспользуемый ресурс времени, - дополнительно выпускаемые валы,   - дополнительно выпускаемые втулки

Согласно модели в системе число неизвестных n=5, число уравнений m=3. Решаем задачу симплекс-методом.

1.  Переменные х₄, х₅ считаем свободными. В качестве базисных

переменных, выраженных через свободные, возьмем х₁, х₂, х₃. Составим опорный план:

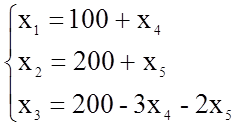
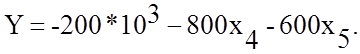
Коэффициенты при х₄, х₅ отрицательные, следовательно, опорный план не оптимален. Переходим к построению нового опорного плана.

2.  Из целевой функции видно, что в разряд базисных целесообразно перевести переменную х₄, а х₅ оставить свободной. Из числа базисных переменных в разряд свободных целесообразно перевести х₃. Тогда новый опорный план будет иметь вид:

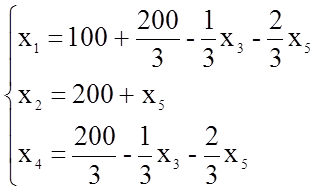
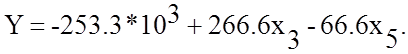
Из целевой функции видно, что коэффициент при х₅ отрицательный, т.е. план не оптимален. Переходим к составлению нового опорного плана.

3.  Из разряда свободных переменных х₅ переводим в базисные, а из базисных переменных х₄ переводим в свободные. Составим опорный план вида:

         

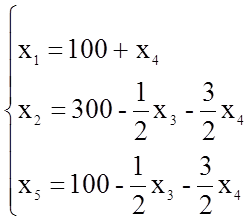
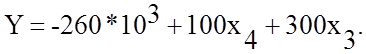
Из целевой функции видно, что опорный план оптимальный. Следовательно х₁=100, х₂=300, х₃=0, х₄=0, х₅=100 и  в соответствии с поставленной задачей необходимо выпустить 100 шт. валов и 300 шт. втулок. При этом будут использованы все ресурсы, и прибыль составит 260 тысяч рублей.

Динамическое программирование

Существуют системы, которые под воздействием управления могут, изменяясь по шагам, переходить из начального состояния  в конечное состояние . Такая система описывается множеством состояний .  В свою очередь каждое состояние  представляет собой -мерное подпространство . Система из состояния  переходит в следующее или конечное состояние под воздействием управления U, которое представляет собой множество . При этом каждое управление  представляет собой -мерное подпространство . В такой системе необходимо выбрать множество управления U таким, чтобы оно с максимальной эффективностью переводило систему из начального состояния S₀ в конечное состояние S_n.