Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 3

Из большого числа теорий и средств моделирования, используемых в качестве математического аппарата, рассмотрим теорию массового обслуживания, имитационное моделирование со средствами планирования и обработки результатов эксперимента, общецелевую систему моделирования GPSS, сети Петри, средства структурного анализа DFD – диаграммы, средства синтеза – линейное и динамическое программирование и теорию игр.

2. 1. Основные понятия систем массового обслуживания

  Под системой массового обслуживания понимается система, которая эффективно распределяет ограниченные ресурсы среди пользователей. В качестве ресурсов могут фигурировать время, материальные ценности, человеческие ресурсы, информационные ресурсы. Система включает в себя:

1)входные потоки пользователей (требовании заявок). Пользователи обращаются к системе за выделение им определённых ресурсов в виде обслуживания;    

2)обслуживающие аппараты (каналы) занимаются распределением ресурсов между пользователями или обслуживанием пользователей. Обслуживающие аппараты часто имеют на своем входе так называемые очереди или средства временного хранения запросов пользователей. Время нахождения пользователя в очереди определяется пропускной способностью обслуживающего аппарата или объёмом имеющихся у него ресурсов;

3)дисциплина обслуживания это правило, по которому пользователь изымается из очереди на обслуживание; в случае нескольких обслуживающих аппаратов привлекаются каналы к обслуживанию, а также регламентируется обслуживание.

     В дальнейшем в качестве ресурсов будем рассматривать ресурс времени. В этом случае в качестве характеристик элементов системы используются для входных потоков – момент обращения i – го  пользователя к системе  t_i. Обслуживающие аппараты характеризуются временем обслуживания _i^o. Если есть очередь, то в качестве ее характеристики используется _i^ож – время нахождения i-го пользователя в очереди или используется  средняя длина в очереди . В качестве общей характеристики системы используется время пребывания _i^пр.

     Системы, в которых проводится один акт обслуживания, называются однофазными системами. Системы, в которых проводится несколько актов обслуживания, называются многофазными.

     В системах может быть несколько обслуживающих аппаратов, которые расположены функционально последовательно (многофазные системы) или параллельно. В этом случае каждый из обслуживающих аппаратов проводит однотипное обслуживание.

     Различают три вида систем обслуживания:

1.Система с отказом. Такая система не имеет очереди. Пользователь при обращении к  занятой системе получает отказ.

2.Система с ограниченной очередью. В таких системах пользователь получает отказ в том случае, если очереди обслуживающих аппаратов заняты.

3. Система без отказов (неограниченная очередь). В таких системах пользователь не получает отказ, и при этом он может находиться в очереди неограниченное время.

     В качестве характеристик системы, определяемых с помощью теории массового обслуживания, используется:

1) для системы с отказом: вероятность  отказа R, вероятность обслуживания пользователя Q, иногда среднее число пользователей, получивших отказ N_отк ;

2) для системы с ограниченной очередью: вероятность обслуживания пользователя Q, среднее время ожидания ^ож , средняя длина очереди ;

3) для системы без отказа: вероятность обслуживания пользователя Q, среднее

время ожидания ^ож , среднее время пребывания _пр.

     Основные дисциплины обслуживания:

1.Правило выбора пользователя из очереди:

         а) пользователь выбирается в порядке очереди;

         б) пользователь из очереди выбирается по жребию (по вероятности), в первую очередь выбирается тот пользователь, вероятность которого больше;

         в) пользователь выбирается из очереди по минимально допустимому времени ожидания.

2.Правило привлечения каналов к обслуживанию. В каналах ведётся обслуживание по различным приоритетам. Приоритет может быть абсолютным и относительным. При абсолютном приоритете пользователь принимается к обслуживанию вне зависимости от состояния системы (занята или свободна). Если система занята, то обслуживание прерывается и система освобождается для обслуживания пользователя с абсолютным приоритетом. При относительном приоритете пользователь принимается к обслуживанию только после обслуживания предыдущего пользователя.

     Каналы привлекаются к обслуживанию:

             1)по очереди;

             2)по жребию;

             3)в порядке номеров;

             4)по максимальной производительности.

2. 1. 1. Моделирование потоков

 Поток представляет собой последовательность однородных событий. Под событием понимается обращение к системе пользователей, требований, заявок и   т. д.  Потоки бывают двух видов: 1)регулярные, когда интервал времени между событиями заранее определен (в детерминированных системах); 2)случайные, когда время наступления события случайно.

     Моделью потока является математическая запись вероятности наступления события потока или математическая запись времени наступления события t_1, t_2, …t_n.

      Если целью моделирования потока является определение вероятности наступления, то в простейшем случае (простейшие потоки) пользуются распределением Пуассона. Распределение Пуассона позволяет найти вероятность наступления числа k событий за интервал времени τ.

     Формула Пуассона:

                        .

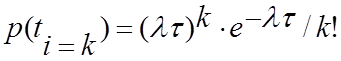С помощью этой формулы определяется вероятность того, что за интервал  времени t к системе будет k обращений с интенсивностью  l (число обращений в единицу времени).

     Указанная формула математически определяет простейший поток. Простейшим потоком называется стационарный, ординарный поток, в котором отсутствует последействие.

     Условие стационарности. Поток стационарный, если в нём вероятность появления k-событий не зависит от времени, а зависит от интервала времени t (см. формулу Пуассона).